原文地址:https://blog.csdn.net/qq_34454069/article/details/77779300
定义:
欧拉回路:每条边恰好只走一次,并能回到出发点的路径
欧拉路径:经过每一条边一次,但是不要求回到起始点
无向图
首先,在无向图中,要确定是否存在欧拉回路很容易:只要每个点的度数均为偶数即可。(这里就不扯什么连不连通的鬼东西了)。
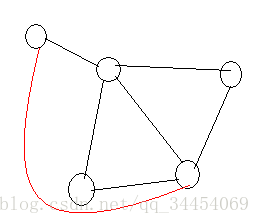
因为每个点的度数为偶数,所以可以将整个图看做由数个环嵌套而成,因为环一定能找到一条欧拉回路,所以整个图也能找到欧拉回路。 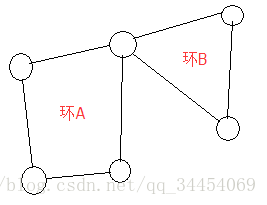
欧拉路径:如果有且仅有两个点的度数为奇数,就会存在一条从这两个中的一个到达另一个的欧拉路径。
假如在这两个点间连一条边,就能够从任意一个点出发找到一条欧拉回路,当出发点为这两个点中的一个时,切断这条边,就成为一条欧拉路径了。
有向图
欧拉回路:所有点的入度等于出度,就存在一条欧拉回路。
这里可以换一种角度来理解,对于每一个点,每次进入这个节点,就一定有一条路可以出去,因此必定存在一条欧拉回路。
欧拉路径:最多有一点入度等于出度+1,最多有一点入度等于出度-1,就会有一条从出度大于入度(没有则等于)的点出发,到达出度小于入度(没有则等于)的点的一条欧拉路径。证明方法与无向图的欧拉路径类似。