历史:
在稀疏表示理论未提出前,正交字典和双正交字典因为其数学模型简单而被广泛的应用,然而他们有一个明显的缺点就是自适应能力差,不能灵活全面地表示信号,1993年,Mallat基于小波分析提出了信号可以用一个超完备字典进行表示,从而开启了稀疏表示的先河
背景:
在20年中,信息稀疏表示,信息处理领域广受关注
目的:
在一个超完备字典中,用尽可能少的原子来表示,从而获得更简单的表达方式,这对信息的处理,压缩,编码及其有用。我的理解是,在一堆要表达的信息中,我们希望用最少的原料来表示这一堆中任何一个信息样例,这有点像坐标的基,只不过这里稀疏表达可能允许工程近似。譬如,一个平面上的点信息,有无数个点,而我建立坐标系之后(甚至不是正交的,只要不平行),我可以轻而易举地用两个坐标变量或者一个二维向量表示这堆点中的任何一个。
研究的重点:
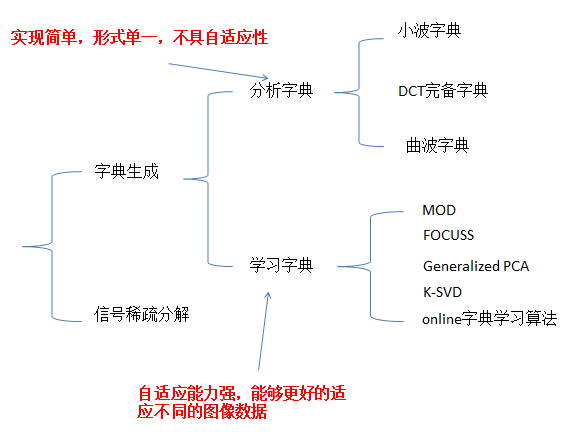
稀疏分解算法、超完备原子字典、和稀疏表示的应用等方面
研究的两大任务:
怎么用数学描述?
定量的分析,我们希望输入经过编码器之后,输出是稀疏的,即只有少量响应为1,其他的为零。对于自然图像(人一生中见过的所有经典的自然图像,门,苹果等),我们得到的输出很显然不是多得不行。更特殊地,我们识别某一种或者几种物体时,不指望我们的描述是“无损的”,也许在低层希望能够接近无损,但到了搞错,最近为了描述特定的几种,而允许大量的“有损”。实际中,输入的图是自然图像,排除了大量的非图情况,省了许多编码代价。
强调一次,我们希望输入经过编码器之后,输出是稀疏的,即只有少量响应为1或靠近1,其他的为零或接近零。这样,我们一个可能的数学描述是:
