并查集

关于并查集的算法，其实也比较简单，主要分为三个步骤，初始化，查找和合并。查找即查找根结点，合并就是合并两个根节点。

并查集通常用于有n个元素的集合应用问题中，在开始时让每个元素构成一个单元素的集合，然后按照一定顺序将属于同一组的元素所在集合合并。

以蓝桥杯中，合根植物一题为例子：

问题描述

　　w星球的一个种植园，被分成 m * n 个小格子（东西方向m行，南北方向n列）。每个格子里种了一株合根植物。
　　这种植物有个特点，它的根可能会沿着南北或东西方向伸展，从而与另一个格子的植物合成为一体。


　　如果我们告诉你哪些小格子间出现了连根现象，你能说出这个园中一共有多少株合根植物吗？

输入格式

　　第一行，两个整数m，n，用空格分开，表示格子的行数、列数（1<m,n<1000）。
　　接下来一行，一个整数k，表示下面还有k行数据(0<k<100000)
　　接下来k行，第行两个整数a，b，表示编号为a的小格子和编号为b的小格子合根了。


　　格子的编号一行一行，从上到下，从左到右编号。
　　比如：5 * 4 的小格子，编号：
　　1 2 3 4
　　5 6 7 8
　　9 10 11 12
　　13 14 15 16
　　17 18 19 20

样例输入

5 4
16
2 3
1 5
5 9
4 8
7 8
9 10
10 11
11 12
10 14
12 16
14 18
17 18
15 19
19 20
9 13
13 17

样例输出

5

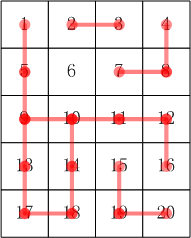
样例说明

　　其合根情况参考下图

 

 

#include<iostream>
using namespace std;
int pre[1000010];

int find(int x)//查找某一元素的根结点
{
    int temp,p;
    p=x;
    while(x!=pre[x])
    {
        x=pre[x];//根节点为x
    }
    while(p!=x)//路径压缩
    {
        temp=pre[p];记录上一级
        pre[p]=x;//把上一级改为根节点
        p=temp;
    }
    return x;
}

int main()
{
    int m,n;
    int i=0;
    cin>>m>>n;//输入行和列
    int k;
    cin>>k;//k行数据
    int sum=m*n;
    for(i=0;i<m*n;i++)
    {
        pre[i]=i;//初始化每个元素为一个集合即其根为自己本身
    }
    for(i=0;i<k;i++)
    {
        int a,b;
        int aa,bb;
        cin>>a>>b;
        aa=find(a);
        bb=find(b);
        if(aa!=bb)
        {
            pre[aa]=pre[bb];//合并根节点
            sum--;
        }
    }

    cout<<sum;
}