一些定义:
1.一个连通且无回路的无向图称为树.
2.若图G的生成子图是一棵树,则该树称为G的生成树.
3.在图G的所有生成树中,树权最小的那棵生成树,称作最小生成树.
关于找出最小生成树的两种算法,一个称为Kruskal(克鲁斯卡尔),另一个叫Prim(普里姆)
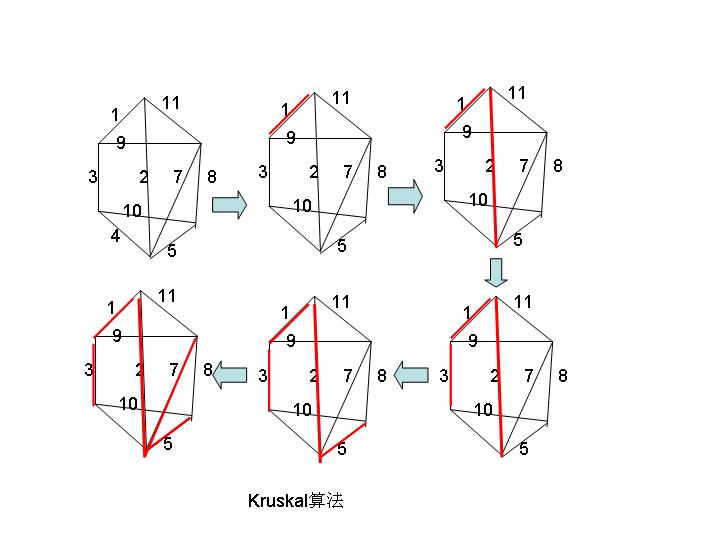
(1) Kruskal 算法
step1: 选取最小权边e1, 置边数i=1
step2: 若 i=n-1 结束,否则转到step3
step3: 设已选择边为e1,e2,...ei 在 G中选取不同于e1,e2,...,ei的边, 使{e1,e2,...,ei,ei+1}中无回路且ei+1是满足此条件的最小边.
step4: i= i+1 转 step2
一句话记住此算法: 在保证无回路前提下选n-1条最小权边.
如下图演示了此算法.
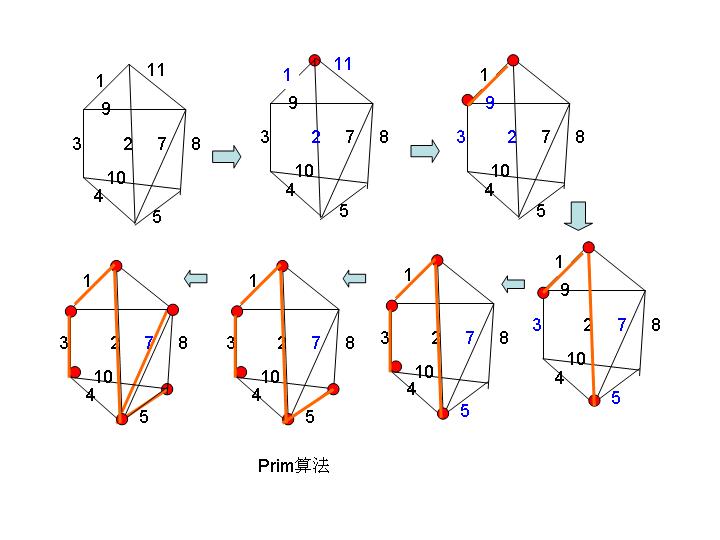
(2) Prim算法(普里姆算法)
step1: 找出存在最小权边的点.
step2: 若所有顶点已经过完,则结束.否则跳step3
step3: 通过已存在的点构成的树来计算出此树到其它未到达的点的最小权.
step4: 选取step3中标记的最小权边的顶点.转至step2.
注:此步骤为自己总结的,如有错误请指正.^_^
比较优劣:
从二者的原理来看,Kruskal是基于边的算法,Prim是基于顶点的.因此对于一个边数很多的图,用Kruskal算法不明智.而顶点多边少的图用Kruskal效率多了
(转)http://www.cnblogs.com/zimmerman/archive/2007/10/06/915704.html