命题:设计一个三变量表决器。真值表如下:

可以写出并简化得出公式:F=AB+BC+AC。
以下是两种算法:
第一种:仅从算法方面描述为:A、B、C的和大于1则输出结果为1,否则为0;源码如下:
module vote_c(a,b,c,result); input a,b,c; output result; reg result; always @(a or b or c or result) begin if((a+b+c)>1) result=1; else result=0; $display("a,b,c,result"); $display("%d,%d,%d,%d",a,b,c,result); end endmodule
第二种:采用上面公式描述的组合逻辑。源码如下:
module vote_d(a,b,c,result); input a,b,c; output result; assign result=((a&&b)||(b&c)||(a&&c)); always@(a or b or c or result) begin $display("a b c result"); $display("%d %d %d %d",a,b,c,result); end endmodule
测试平台 modelsim altera 6.5b,测试源码如下:
`timescale 1us/1us `include "votec.v" `include"voted.v" module vote_top; reg a,b,c; wire result; initial begin a=0;b=0;c=0; #10 a=0;b=0;c=1; #10 a=0;b=1;c=0; #10 a=0;b=1;c=1; #10 a=1;b=0;c=0; #10 a=1;b=0;c=1; #10 a=1;b=1;c=0; #10 a=1;b=1;c=1; end vote_c v1(a,b,c,result); //vote_d v2(a,b,c,result); endmodule
得出结果都为:
# a b c result
# 0 0 0 0
# a b c result
# 0 0 1 0
# a b c result
# 0 1 0 0
# a b c result
# 0 1 1 1
# a b c result
# 1 0 0 0
# a b c result
# 1 0 1 1
# a b c result
# 1 1 0 1
# a b c result
# 1 1 1 1
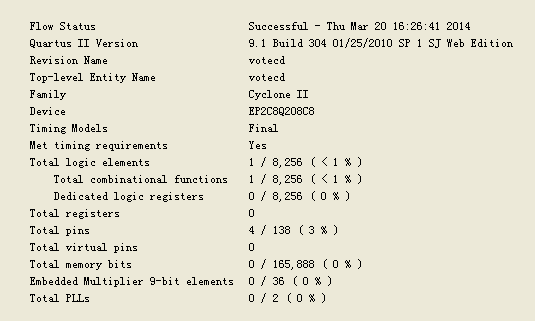
与真值表一致。所以两种方式都是正确的。在quartus II中综合编译后:
第一种的RTL视图如下:
可以看出,该模块综合成两个加法器和一个比较器。
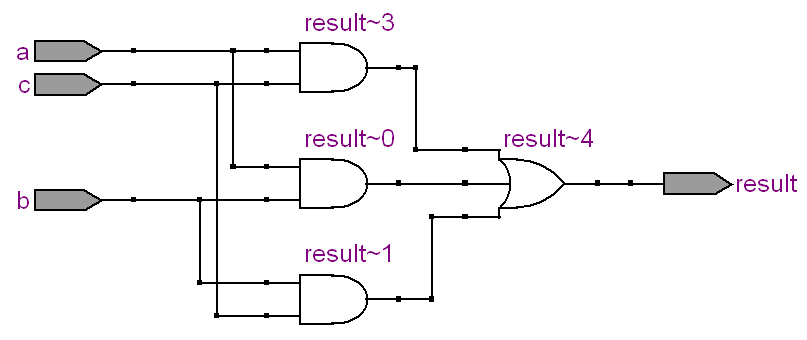
第二种RTL视图如下:
可以看出综合成3个与门和一个或门的组合逻辑电路。
两者在资源消耗方面如下:
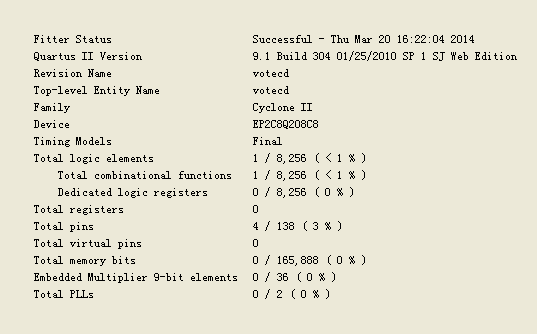
可以看出基本没有区别。仿真器应该最后将他们优化成一致了。