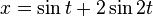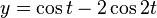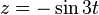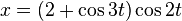终于将二维图形发完了,从这一节开始,步入3D的图形世界.
相关软件参见:数学图形可视化工具,使用自己定义语法的脚本代码生成数学图形.该软件免费开源.QQ交流群: 367752815
以下是维基中对三叶结的介绍:
在纽结理论中,三叶结(trefoil knot)是一种最简单的非平凡纽结。可以用反手结连接两个末端而达成。它是唯一一种有3个交叉的纽结。它也可以描述为环面纽结。由于三叶结的结构极为简单,它是研究纽结理论很重要的基本案例,在拓扑学、几何学、物理学、化学领域,有广泛的用途。
三叶结可以由以下的参数方程确定:
三叶结也可以看作环面纽结。对应的参数方程为:
针对如上两种数学公式对应的脚本代码如下:
#http://zh.wikipedia.org/wiki/%E4%B8%89%E5%8F%B6%E7%BB%93 vertices = 1000 t = from 0 to (2*PI) x = sin(t) + 2*sin(2*t) y = cos(t) - 2*cos(2*t) z = -sin(3*t) r = 10; x = x*r y = y*r z = z*r
vertices = 1000 t = from 0 to (2*PI) x = (2 + cos(3*t))*cos(2*t) y = (2 + cos(3*t))*sin(2*t) z = sin(3*t) r = 10; x = x*r y = y*r z = z*r
不过两种写法生成的图形不太一样:


让我们再看一下公式:
x = sin(t) + 2*sin(2*t)
y = cos(t) - 2*cos(2*t)
我想可以将其改为
x = sin(t) + v*sin(2*t)
y = cos(t) - v*cos(2*t)
其中v是一个变化的数,取值范围为[-5,5]
那么由此可以生成一个曲面,亦可以通过我的软件看到每一个参数值下的三叶结是什么样子:
vertices = D1:360 D2:100 u = from 0 to (2*PI) D1 v = from -5 to 5 D2 x = sin(u) + v*sin(2*u) y = cos(u) - v*cos(2*u) z = -sin(3*u) r = 10; x = x*r y = y*r z = z*r