从这一节开始讲3D的数学图形,为此我准备了好久.这一节中将为你展示如何生成球面,椭球面,胶囊体,刺球,圆弧面.
相关软件参见:数学图形可视化工具,使用我自定义语法的脚本代码生成数学图形.
在我刚学计算机图形学的时候,就写过生成球面的程序,代码曾发布在球(Sphere)图形的生成算法.
球与圆很相关,一个是三维,一个是二维,可以参考下:圆,椭圆
(1)sphere的第一种写法
vertices = D1:100 D2:100 t = from 0 to (PI*2) D1 r = from 0 to 1 D2 x = 2*r*sin(t)*sqrt(1-r^2) y = 2*r*cos(t)*sqrt(1-r^2) z = 1-2*(r^2)

球的网格线:
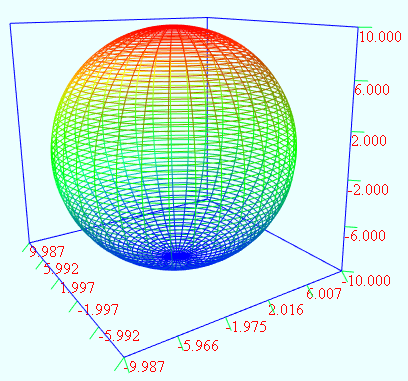
(2)sphere的另两种写法
vertices = dimension1:36 dimension2:72 u = from 0 to (2*PI) dimension1 v = from (-PI*0.5) to (PI*0.5) dimension2 r = 10.0 x = r*cos(v)*sin(u) y = r*sin(v) z = r*cos(v)*cos(u)
vertices = dimension1:36 dimension2:72 u = from 0 to (2*PI) dimension1 v = from 0 to (PI) dimension2 r = 10.0 x = r*sin(v)*sin(u) y = r*cos(v) z = r*sin(v)*cos(u)
两种写法生成的图形是一样的

(3)彩色球
在脚本中给rgb变量设值,就能设置顶点色.
vertices = dimension1:72 dimension2:72 u = from 0 to (2*PI) dimension1 v = from (-PI*0.5) to (PI*0.5) dimension2 x = cos(v)*sin(u) y = sin(v) z = cos(v)*cos(u) a = 10.0 r = (x+1.0)/2 g = (y+1.0)/2 b = (z+1.0)/2 x = a*x y = a*y z = a*z

(4)圆弧面
将球的第二维度范围减小,即得到圆弧面
vertices = dimension1:36 dimension2:72 u = from 0 to (2*PI) dimension1 v = from (PI*0.1) to (PI*0.5) dimension2 r = 10.0 x = r*cos(v)*sin(u) y = r*sin(v) z = r*cos(v)*cos(u)


(5)椭球面
#http://www.mathcurve.com/surfaces/ellipsoid/ellipsoid.shtml vertices = D1:100 D2:100 u = from 0 to (2*PI) D1 v = from (-PI*0.5) to (PI*0.5) D2 a = rand2(1, 10) b = rand2(1, 10) c = rand2(1, 10) x = a*cos(v)*sin(u) y = b*sin(v) z = c*cos(v)*cos(u)

(6)胶囊体
将球面向上下两头拉伸,即得到胶囊体,我也曾经写过胶囊体的生成算法胶囊体(Capsule)图形的生成算法

(7)刺球
将球面上顶点到球心的距离,有规律地变化,可以得到多变的球,如刺球
vertices = dimension1:129 dimension2:65 u = from 0 to (2*PI) dimension1 v = from (-PI*0.5) to (PI*0.5) dimension2 n =4 a = from 0 to 128 D1 b = from 0 to 64 D2 t = (mod(a, n) + mod(b, n))/n*4 r = 10.0 + t x = r*cos(v)*sin(u) y = r*sin(v) z = r*cos(v)*cos(u)
