前几天,有个同事看到我生成的一幅逻辑斯蒂分岔图像后,问我:“这是咪咪吗?”我回答:“淫者见淫。”好吧,这里将生成几种分岔映射图形,包括逻辑斯蒂映射系统,正弦映射系统和曼德勃罗映射系统。实际上这几种图形算不上分形,只不过它与我写的其他分形对象使用相同的基类,所以也将其列入混沌分形的范畴。
关于基类FractalEquation的定义及相关软件见:混沌与分形
(1)逻辑斯蒂映射系统
// 逻辑斯蒂映射系统
class LogisticMap : public FractalEquation
{
public:
LogisticMap()
{
m_StartX = 0.0f;
m_StartY = 0.0f;
m_StartZ = 0.0f;
m_ParamA = 0.0f;
m_ParamB = 4.0f;
m_nIterateCount = 100;
}
void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
{
float R = (float)rand()/RAND_MAX;
float k = m_ParamA + (m_ParamB - m_ParamA) * R;
outX = R*4.0f;
outY = (float)rand()/RAND_MAX;
for (int i = 0; i < m_nIterateCount; i++)
{
outY = k*outY*(1-outY);
}
outY *= 2;
outZ = z;
}
bool IsValidParamA() const {return true;}
bool IsValidParamB() const {return true;}
private:
int m_nIterateCount;
};

调节下参数后的图形:
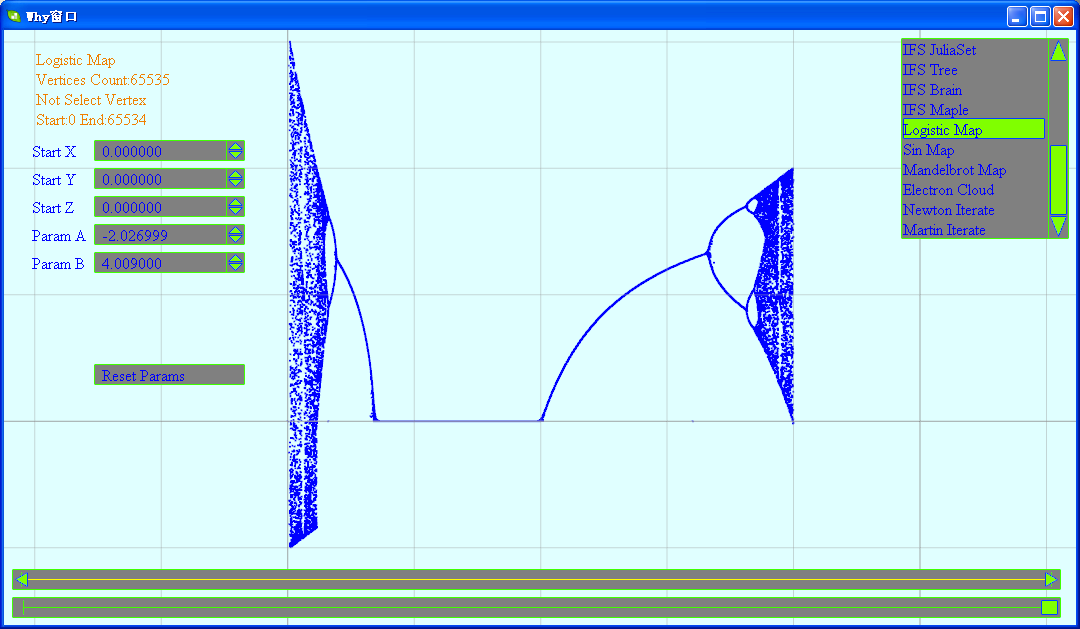
(2)正弦映射系统
// 正弦映射系统
class SinMap : public FractalEquation
{
public:
SinMap()
{
m_StartX = 0.0f;
m_StartY = 0.0f;
m_StartZ = 0.0f;
m_ParamA = -2*PI;
m_ParamB = 2*PI;
m_nIterateCount = 64;
}
void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
{
float R = (float)rand()/RAND_MAX;
float k = m_ParamA + (m_ParamB - m_ParamA) * R;
outX = R*4.0f;
outY = (float)rand()/RAND_MAX;
for (int i = 0; i < m_nIterateCount; i++)
{
outY = k*sinf(outY);
}
outY *= 0.5f;
outZ = z;
}
bool IsValidParamA() const {return true;}
bool IsValidParamB() const {return true;}
private:
int m_nIterateCount;
};

(3)曼德勃罗映射系统
// 曼德勃罗映射系统
class MandelbrotMap : public FractalEquation
{
public:
MandelbrotMap()
{
m_StartX = 0.0f;
m_StartY = 0.0f;
m_StartZ = 0.0f;
m_ParamA = -2.0f;
m_ParamB = 0.0f;
m_nIterateCount = 64;
}
void IterateValue(float x, float y, float z, float& outX, float& outY, float& outZ) const
{
float R = (float)rand()/RAND_MAX;
float k = m_ParamA + (m_ParamB - m_ParamA) * R;
outX = R*4.0f;
outY = (float)rand()/RAND_MAX;
for (int i = 0; i < m_nIterateCount; i++)
{
outY = outY*outY + k;
}
outZ = z;
}
bool IsValidParamA() const {return true;}
bool IsValidParamB() const {return true;}
private:
int m_nIterateCount;
};

最后发下被我同事当成MM的逻辑斯蒂分岔图像:

之前我还写过一篇关于逻辑斯蒂的文章:混沌数学之logistic模型