AGC 043 B

题目：传送门

题意：

给你一个长度为 N 的只由123 构成的字符串 a ，定义 Xi,j 满足：

 

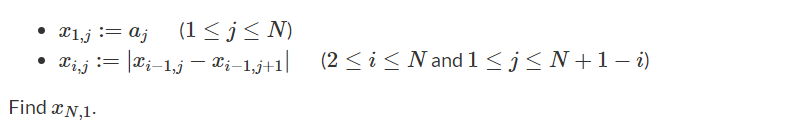
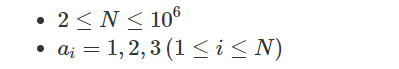
思路：

推荐博客：博one   博two

第一个观察，最终的答案只可能是 0、1、2，然后，从 N = 2 起，Xi,j 就不存在 3 了，都是 0、1、2，那我们直接在输入的时候，就将 123 转换为 012 是可以的，因为 N >= 2 嘛。

第二个观察，若字符串中存在 1 ，那么它的最终答案就不可能是 2，因为你 2 遇到 1 会变为 1，你 0 遇到 1 也会变成 1，你只要 1 和 0 或者 2 同时存在，你的 1 就不可能消掉，那就考虑最终答案是 0 或者 1，也就是考虑最终答案的奇偶性就行了。这时，需要注意到，在 mod 2 的运算中，减法，相当于加法。那么题目给的递推式就变成了：

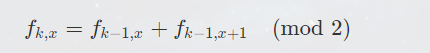（截取自 博two）

到此，你就需要有一定的经验了，你需要发现，这个式子很像求组合数的递推公式：

C(n,m)=C(n−1,m−1)+C(n - 1,m)

只不过，递推的方向不同.

由于在 mod 2 下减法相当于加法，那我们只需要知道，输入的字符串，每个数被加了几次即可，第 i 个数被加的次数就是 C(n - 1, i - 1).

由于 n <= 1e6 很大，可以用 Lucas 定理去求组合数，也可以根据

C(n, m) = n! / ( m! * (n - m)! )

我们只想要知道 C(n, m） 的奇偶性，那我们可以求 n! 中质因子 2 的个数，减去 m! 中质因子 2 的个数，再减去 (n - m)! 中质因子 2  的个数，若减完之后等于 0，那么C(n, m) 就是奇数，否则说明C(n, m) 有质因子 2 ，那他就是偶数。

第三个观察，若字符串中不存在 1，也就是说只有 0 和 2，这时只要把 2 看成 1 就行了，若最终答案是奇数，就是输出 2 ，否则就输出 0.

#include <bits/stdc++.h>
#define LL long long
#define ULL unsigned long long
#define mem(i, j) memset(i, j, sizeof(i))
#define rep(i, j, k) for(int i = j; i <= k; i++)
#define dep(i, j, k) for(int i = k; i >= j; i--)
#define pb push_back
#define make make_pair
#define INF INT_MAX
#define inf LLONG_MAX
#define PI acos(-1)
using namespace std;

const int N = 1e6 + 5;

const LL mod = 1e9 + 7;

LL ksm(LL a, LL b) { LL ans = 1LL; while(b) { if(b & 1) ans = ans * a % mod; a = a * a % mod; b >>= 1; }  return ans; }

char a[N];
int fac[N];

void init(int n) {
    fac[0] = 0;
    rep(i, 1, n) {
        fac[i] = fac[i - 1];
        int tmp = i;
        while(tmp % 2 == 0) {
            fac[i]++;
            tmp = tmp / 2;
        }
    }
}

int C(int n, int m) {
    return fac[n] - fac[m] - fac[n - m];
}

void solve() {

    int n;

    scanf("%d", &n);

    scanf("%s", a + 1);

    bool flag0 = 0, flag1 = 0, flag2 = 0;

    rep(i, 1, n) {
        a[i]--;
        if(a[i] == '0') flag0 = 1;
        if(a[i] == '1') flag1 = 1;
        if(a[i] == '2') flag2 = 1;
    }
    if(flag0 + flag1 + flag2 <= 1) {
        puts("0"); return ;
    }

    init(n);

    int ans = 0;
    if(flag1) {
        rep(i, 1, n) {
            if(a[i] == '1') {
                if(C(n - 1, i - 1) == 0) ans ^= 1;
            }
        }
    }
    else {
        rep(i, 1, n) {
            if(a[i] == '2') {
                if(C(n - 1, i - 1) == 0) ans ^= 1;
            }
        }
        ans = ans * 2;
    }
    printf("%d
", ans);
}


int main() {
//    int _; scanf("%d", &_);
//    while(_--) solve();
//
    solve();

    return 0;
}