题目:传送门
题意
已知一个圆心在原点O的圆的半径,给你两个点P,Q,|PO| == |DO|,P,Q不在圆外。在圆上取一点D,求 |PD| + |QD| 的最小值。
思路
点在圆内,会比较难处理,若点在圆外,则只需分两种情况即可:
1.直线PQ和圆相交,那么D一定是直线PQ和圆的交点中的任意一个,那答案就是 |PQ|;
2.直线PQ和圆想离,那么D一定是直线PQ的垂直平分线与圆的交点。
考虑怎么将圆内的点转移到圆外去。根据圆的反演的性质,在圆内的点反演后变为在圆外的点。
故把给定的圆作为反演圆,反演PQ,然后就是分成上面的两种情况。
还需要特判一下点 P,Q 重合的情况和点 P,Q在圆上的情况。
证明一下为什么将 P,Q 反演为 P',D'后,求 PD + QD 的最小值可以转化为求 P'D + Q'D 的最小值:
假设我们已经求出P,Q的反演点 P‘,Q’,由反演的性质有三角形P‘OD与三角形DOP相似;
PD = PO*P'D / r 同理有 QD = QO * Q'D / r;
其中PO == DO,那么有
PD + QD = PO / r * (P'D + Q'D)
PO / r 是一个定值,那么求PD + QD的最小值实际上也是求 P'D + Q'D的最小值。
下面介绍一下,直线与圆相离,求P'D + Q'D 的最小值的方法:
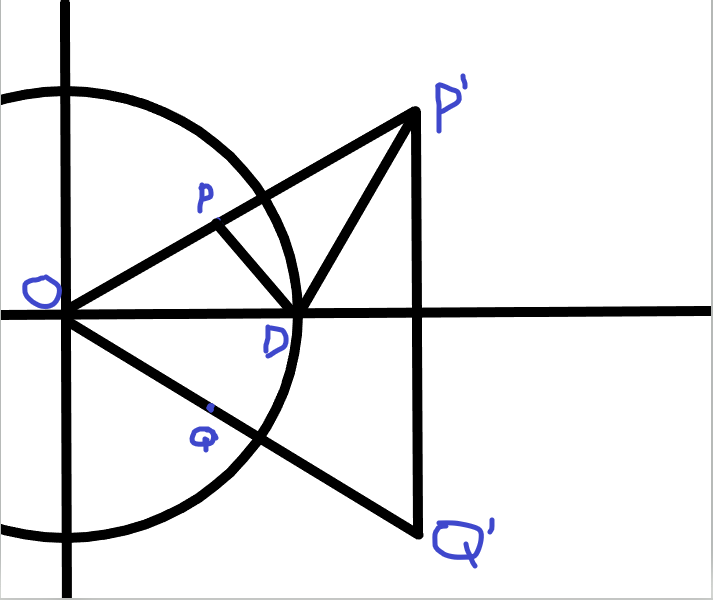
对于直线P'Q'和圆相离的情况,考虑怎么求P'D+Q'D的最小值
首先可以通过 OP' * OD' = |OP'| |OD'| * cos(角P'OD') (OP' * OD' 表示向量OP’和向量OD'的点积)求得 角P'OD' 的一半。
然后在三角形ODP'里面,我们已知角P'OD和边OP'和边OD,那么通过余弦定理可求得边DP‘,又 DP' = DQ',故求得 DP' + DQ'
#include <bits/stdc++.h> #define LL long long #define ULL unsigned long long #define UI unsigned int #define mem(i, j) memset(i, j, sizeof(i)) #define rep(i, j, k) for(int i = j; i <= k; i++) #define dep(i, j, k) for(int i = k; i >= j; i--) #define pb push_back #define make make_pair #define INF 0x3f3f3f3f #define inf LLONG_MAX #define PI acos(-1) #define fir first #define sec second #define lb(x) ((x) & (-(x))) #define dbg(x) cout<<#x<<" = "<<x<<endl; using namespace std; const int N = 1e6 + 5; const double eps = 1e-8; struct Point { double x, y; Point(double a = 1.0, double b = 1.0) : x(a), y(b) {} Point operator + (const Point &a) { return Point(x+a.x, y+a.y); } Point operator - (const Point &a) { return Point(x-a.x, y-a.y); } Point operator * (const double a) { return Point(a*x, a*y); } Point operator / (const double a) { return Point(a/x, a/y); } void Input() { scanf("%lf %lf", &x, &y); } void Output() { printf("%.8f %.8f ", x, y); } }; struct Circle { Point o; double r; Circle(Point a = Point(), double b = 1.0) : o(a), r(b) { } Point getPoint(double alpha) { return o + Point(r*cos(alpha), r*sin(alpha)); } void Input() { o.Input(); scanf("%lf", &r); } void Output() { printf("%.8f %.8f %.8f ", o.x, o.y, r); } }; double Dot(Point A, Point B) { return A.x * B.x + A.y * B.y; /// 点积 } double Length(Point A) { return sqrt(Dot(A, A)); } double dis(Point a, Point b) { return sqrt((a.x-b.x) * (a.x-b.x) + (a.y-b.y) * (a.y-b.y)); } double Cross(Point a, Point b, Point c) { return (b.x-a.x)*(c.y-a.y) - (c.x-a.x)*(b.y-a.y); } double Cross(Point a, Point b) { return a.x*b.y - a.y*b.x; } double Dot(Point a, Point b, Point c) { return (b.x-a.x)*(c.x-a.x) + (b.y-a.y)*(c.y-a.y); } int dcmp(double x) { return (x > eps) - (x < -eps); } bool operator == (Point A, Point B) { return dcmp(A.x-B.x) == 0 && dcmp(A.y - B.y) == 0; } Point Point_Inver(Circle c0,Point P){ Point OP = P - c0.o; double len = dis(c0.o,P); len = len*len; return c0.o + OP*( c0.r * c0.r / len ); } Circle Circle_Inver(Circle c0,Circle a){ Circle res; Point OA = a.o - c0.o; double len = dis(a.o,c0.o); Point up = c0.o + OA * ( ( len + a.r) / len ); Point down = c0.o + OA *( (len - a.r) / len ); up = Point_Inver(c0,up); down = Point_Inver(c0,down); res.o = (up+down) * 0.5; res.r = dis(up,down) * 0.5; return res; } Circle Line_Inver(Circle c0,Point a,Point b){ Circle res = Circle(); double d = fabs(Cross(a,c0.o,b) / dis(a,b)); res.r = c0.r * c0.r / (2.0 * d); double len = Dot(a,b,c0.o) / dis(a,b); Point AB = b - a; Point c = a + AB * (len/dis(a,b)); Point CO = c - c0.o; res.o = c0.o + CO * (res.r/d); //double len = dis(a,c[1].o); //res.o = c0.o + (a-c[1].o) * (res.r/len); return res; } double DistanceToSegment(Point p, Point A, Point B) { /// 求点 p 到线段 AB 的最短距离 if(A == B) return Length(p - A); Point v1 = B - A, v2 = p - A, v3 = p - B; if(dcmp(Dot(v1, v2)) < 0) return Length(v2); else if(dcmp(Dot(v1, v3)) > 0) return Length(v3); else return fabs(Cross(v1, v2)) / Length(v1); } Circle c0; Point P, Q; void solve() { c0.o = Point(0, 0); scanf("%lf", &c0.r); P.Input(); Q.Input(); double rate = dis(P, Point(0, 0)) / c0.r; if(dcmp(P.x - Q.x) == 0 && dcmp(P.y - Q.y) == 0) { /// 重合 printf("%.8f ", 2.0 * (c0.r - dis(Point(0, 0), P))); } else if(P.x * P.x + P.y * P.y == c0.r * c0.r) { /// 点在圆上 printf("%.8f ", dis(P, Q)); } else { P = Point_Inver(c0, P); Q = Point_Inver(c0, Q); /// 点重演 if(dcmp(DistanceToSegment(Point(0, 0), P, Q) - c0.r) > 0) { /// 直线PQ和圆相离 double D=dis(P,Point(0, 0)); double ang=acos(Dot(P,Q)/(D*D))/2.0; /// 求得角的一半 printf("%.8f ", rate * 2.0*sqrt(c0.r*c0.r+D*D-2*c0.r*D*cos(ang))); ///余弦定理 } else { /// 相交 printf("%.8f ", rate * dis(P, Q)); } } } int main() { int _; scanf("%d", &_); while(_--) solve(); // solve(); return 0; }