hdu6438-hdu6447
左转官方题解
1001Buy and Resell(思维)
i点和它后面的谁交易不影响答案,如样例一中的(10-1 + 9-2)=(9-1 + 10-2)
考虑第 i 天是否卖出,一定是在左边列的前 i - 1 个中找一个还未配对的最小值和其配对进行买卖获益最大,如果最小值 >= 当前第 i 天的价格就不交易。用堆维护已买的东西,对于这样一情况,有 i,j,k,m点,在 i 点买入东西后,先打算在 j 点卖出,这时候添加两次 j 点到堆中,因为如果后来的第一次碰到比 j 大的点k是让 j 作为中转点,实际是i和k交易,第二次碰到比 j
大的点m是让m与 j 交易了!!!

#include<bits/stdc++.h> #define per(i,a,b) for(int i=a;i<=b;i++) #define mod 1000000007 using namespace std; typedef long long ll; const int inf =0x3f3f3f3f; const double eps=1e-8; #define siz 100005 int T,n,a,x; struct Node{ int w,d;//d用来表示是第几次用到了,d==0则交易次数要+=2 Node(int a,int b):w(a),d(b){} //有了构造函数后就可以用{*,*}构造一个没名字的对象 bool operator<(const Node &rhs)const{//rhs right hand side 表达式的右边值 //这里&主要是防止值传递的空间浪费,且速度更快 if(w==rhs.w)return d<rhs.d; return w>rhs.w; } }; int main() { scanf("%d",&T); while(T--){ scanf("%d",&n); ll ans=0,cnt=0; priority_queue<Node>que; for(int i=0;i<n;i++){ scanf("%d",&x); Node tmp(0,0); if(!que.empty()&&x>que.top().w){ tmp=que.top(); que.pop(); ans-=tmp.w; ans+=x; if(tmp.d==0)cnt+=2; tmp.w=x;tmp.d=0; que.push(tmp); tmp.w=x;tmp.d=1; que.push(tmp); } else { tmp.w=x; tmp.d=0; que.push(tmp); } } printf("%lld %lld ",ans,cnt); } return 0; }
1003Dream(费马小定理)

#include<bits/stdc++.h> #define per(i,a,b) for(int i=a;i<=b;i++) #define mod 1000000007 using namespace std; typedef long long ll; const int inf =0x3f3f3f3f; const double eps=1e-8; #define siz 100005 int T,p; int main() { scanf("%d",&T); while(T--){ scanf("%d",&p); for(int i=0;i<p;i++){ for(int j=0;j<p;j++){ printf("%lld%c",(long long)(i+j)%p," "[j==p-1?1:0]); } } for(int i=0;i<p;i++){ for(int j=0;j<p;j++){ printf("%lld%c",((long long)i*j)%p," "[(j!=p-1)?0:1]); } } } return 0; }
1004Find Integer(费马大定理,奇偶数列法则)
列出 i 为1 2 3 4 。。。时i^2的值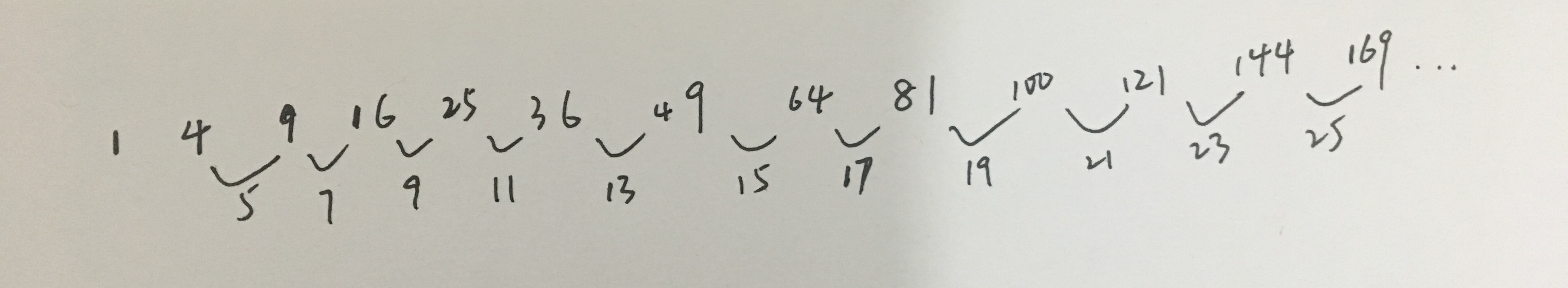
会发现,a为奇数时,会只有有差值存在,a为偶数时两个差值相加即可,①a为奇数时,对于每个b,它跟后面的值的差值是3+(b-1)*2,所以a^2=3+(b-1)*2 , b=(a^2-3)/2+1=2*n^2+2*n
c=b+1 ②a为偶数时,对于每个b,它后面两个差值的和为4+4*b , a^2=4+4*b , b=(a^2-4)/4 , c=b+2
费马大定理中a^n+b^n=c^n n>=3是不成立就是因为存在两数或这多间隔的数的差等于a^3

#include<bits/stdc++.h> #define per(i,a,b) for(int i=a;i<=b;i++) #define mod 1000000007 using namespace std; typedef long long ll; const int inf =0x3f3f3f3f; const double eps=1e-8; #define siz 100005 int T,n,a; int main() { scanf("%d",&T); while(T--){ int b,c; scanf("%d %d",&n,&a); if(n>2||n==0){printf("-1 -1 ");continue;} else if(n==1){ printf("1 %d ",a+1); } else if(n==2){ if((a*a)&1){ b=(a*a-3)/2+1; c=b+1; } else { b=(a*a-4)/4; c=b+2; } printf("%d %d ",b,c); } } return 0; }
1007Neko's loop(同余,循环节)
题目描述有问题,应该是只能走m个点,而不是跳m次
07题意:由模n构成的一个群,每个点有权值(含负数),要求从任意点出发,能经过<=m个点,每次跳跃k格(这是存在循环节的),找出最大的子段和!!!
打表->找规律
这是存在循环节的,且循环节中每个值不同,证明:考虑模n的群,0 1 2 3...n-1,对于任意点 a,列出a,a+k,a+2k,a+3k,......a+xk , 存在i,j a+ik≡a+jk 则k(i-j)≡0(mod n), 如果k,n互质,则只有i==j时成立,如果不互质,则 i-j 是n/gcd(n,k)的倍数则成立,所以x为n/gcd(n,k)时,a≡a+xk(mod n)。所以循环节大小为n/gcd(n,k) !!!
遍历每种循环节,,,找长度小于某个值的区间最大子段和,bin聚模版中的查找<=某长度的最大字段和(含负数)则好使,因为记录了历史点,所以只要当前点的前缀和比历史点的前缀和小,就删去历史点

#include<bits/stdc++.h> using namespace std; #define MOD 998244353 #define per(i,a,b) for(int i=a;i<=b;i++) typedef long long ll; const int N=10005; int T,n,m,k,a[N]; ll s,sum[N*3+5],ans; bool vis[N]; //int b[N*2+5];//记录fun函数中st,ed位置的点是什么 void fun(vector<int>&v){ int bk_siz=v.size();//block_size sum[0]=0; for(int i=1;i<=3*bk_siz;i++)sum[i]=sum[i-1]+a[v[(i-1)%bk_siz]]; int bk=m/bk_siz-1;//如果刚好 m是bk_siz的整数倍那怎么选都一样,因为后面的接到前面是一样的 //如果不是整数倍,那么我们要拿出m%bk_siz+一份bk,这是要安排前后两段 //我们要合理安排m%bk_siz这部分,如n=5且m%bk_siz=3,那我们能通过那最后一段block拿几个点放开头, //使得剩下的拿一个能安排在最大的位置 //所以这里b数组开三倍循环节大小也是这个原因,如果是点123这三点最大,那只需两个循环节就可以找到安放位置, 但是 ,如果是点5 0 1 这三点最大,我们把最后一段安排3个点到开头填充2 3 4点,然后%余下的三个点中有两个安放在0 1点,最后还有一个点就要向前再开一个block喽 !!! if(bk<0)bk=0; ll res1=(ll)bk*sum[bk_siz]; if(res1<0)res1=0; int surp=m-bk*bk_siz;//surplus 剩余能走的点 //if(surp==bk_siz){ans=min(ans,max(0LL,s-res1-max(0LL,sum[bk_siz])));return;} /*int st=0,ed=1; ll res2=0; for(int i=1;i<3*bk_siz;i++){ while(st<i && st+surp<i)st++; while(st<i && sum[st+1]<sum[st])st++;//这种方式不行,因为如果后一位是正数,单数后后为是很小很小的负数 res2=max(res2,sum[i]-sum[st]); //那么st理应至少后后位,但是这种判断方式判断后一位时就跳不过去了!!! }*/ int b[30010]; long long res2= 0; int st, ed; st = 0; ed = 0; b[ed++] = 0; for (int i = 1; i < 3*bk_siz; i++) { while (st < ed && b[st] < i - surp)st++; res2 = max(res2, sum[i] - sum[b[st]]); while (st < ed && sum[b[ed-1]] >= sum[i])ed--; b[ed++] = i; } ans=min(ans,max(0LL,s-res1-res2)); } int main() { scanf("%d",&T); int cas=0; while(T--){ cas++; scanf("%d %lld %d %d",&n,&s,&m,&k); for(int i=0;i<n;i++)scanf("%d",&a[i]); ans=s; memset(vis,false,sizeof(vis)); for(int i=0;i<n;i++){ if(vis[i])continue; vis[i]=true; vector<int>v; v.push_back(i); int now=(i+k)%n; while(now!=i){v.push_back(now);vis[now]=true;now=(now+k)%n;} fun(v); } printf("Case #%d: %lld ",cas,ans); } return 0; }
1009Tree and Permutation
贡献思维,考虑每条边对答案的贡献,以样例一位例,经过e12的有点对12,13,31,21即sz*(n-sz)*2,sz是子树大小,然后将1与其他点结合后,剩下n-1个点,所以每个点对所占的全排列是(n-1)!

#include<bits/stdc++.h> #define per(i,a,b) for(int i=a;i<=b;i++) #define mod 1000000007 using namespace std; typedef long long ll; const int inf =0x3f3f3f3f; const double eps=1e-8; #define siz 100005 int n,head[siz],Enum=0; ll ans=0,jie;//注意这两个一定要开longlong!!! struct Edge{int to,w,ne;}edge[siz*2]; void init(){ ans=0; Enum=0; memset(head,-1,sizeof(head)); jie=1; per(i,2,n-1)jie=jie*i%mod; } void add_edge(int a,int b,int c){ edge[Enum].to=b; edge[Enum].w=c; edge[Enum].ne=head[a]; head[a]=Enum++; } ll dfs(int u,int pre) { ll sz=1,csz=0; ll tmp; for(int i=head[u];i!=-1;i=edge[i].ne){ int v=edge[i].to; if(v==pre)continue; csz=dfs(v,u); tmp=(long long)csz*(n-csz)%mod*2%mod*jie%mod*edge[i].w%mod; ans=(ans+tmp)%mod; sz+=csz; } return sz; } int main() { while(scanf("%d",&n)!=EOF){ init(); int a,b,c; for(int i=1;i<n;i++){ scanf("%d %d %d",&a,&b,&c); add_edge(a,b,c);add_edge(b,a,c); } dfs(1,-1); printf("%lld ",ans); } return 0; }
1010 YJJ's Salesman(dp,树状数组,降维,离散化)
将二维降成一维,一般就是按照第一维度排好序,然后扫描点,此时某点之前扫描过的点的第一维度不会大于该点的第一维!这样就不用考虑第一维度了!!!

#include<bits/stdc++.h> #define per(i,a,b) for(int i=a;i<=b;i++) #define mod 1000000007 using namespace std; typedef long long ll; const int inf =0x3f3f3f3f; const double eps=1e-8; #define siz 100005 struct Node{int x,y,v;}node[siz]; int T,n,num[siz],dp[siz],a[siz],tot; void init() { memset(num,0,sizeof(num)); memset(dp,0,sizeof(dp)); } int lb(int u){return u&-u;} void update(int u,int k) { for(int i=u;i<=tot;i+=lb(i)){ num[i]=max(num[i],k); } } int get_query(int u) { int res=0; for(int i=u;i>0;i-=lb(i)){res=max(res,num[i]);} return res; } bool cmp(Node a,Node b){if(a.x==b.x)return a.y<b.y;else return a.x<b.x;} int main() { scanf("%d",&T); while(T--){ init(); scanf("%d",&n); per(i,1,n){scanf("%d %d %d",&node[i].x,&node[i].y,&node[i].v);} //离散化,记录,排序,去重,重新赋值 tot=0; for(int i=1;i<=n;i++)a[tot++]=node[i].y; sort(a,a+tot); tot=unique(a,a+tot)-a;//离散化,即只把用到的点记录下来,然后把原来的值换成新的离散值,减小循环量 for(int i=1;i<=n;i++){node[i].y=lower_bound(a,a+tot,node[i].y)-a+1;} sort(node+1,node+n+1,cmp); per(i,1,n)dp[i]=node[i].v;// int ans=0,p=1; for(int i=1;i<=n;i++){ while(p<i && node[p].x<node[i].x){ update(node[p].y,dp[p]); p++; } dp[i]=get_query(node[i].y-1)+node[i].v; ans=max(ans,dp[i]); } printf("%d ",ans); } return 0; }
