本文索引目录:
一、PTA实验报告题1 : 程序存储问题
1.1 实践题目
1.2 问题描述
1.3 算法描述
1.4 算法时间及空间复杂度分析
二、PTA实验报告题2 : 删数问题
2.1 实践题目
2.2 问题描述
2.3 算法描述
2.4 算法时间及空间复杂度分析
三、PTA实验报告题3 : 最优合并问题
3.1 实践题目
3.2 问题描述
3.3 算法描述
3.4 算法时间及空间复杂度分析
四、实验心得体会(实践收获及疑惑)
一、PTA实验报告题1 : 程序存储问题
1.1 实践题目:

1.2 问题描述:
题意是,题干给定磁盘总容量和各个文件的占用空间,询问该磁盘最多能装几个文件。
1.3 算法描述:
签到题,只需要将各个文件从小到大排序,并拿一个变量存储已占用的容量总和,进行对比即可得到结果。
#include<bits/stdc++.h> #include<algorithm> using namespace std; #define MAXLENGTH 1000 int interger[MAXLENGTH]; int main() { int num,length; int sum = 0; int counter = 0; int m = 0; cin>>num>>length; for(int i=0;i<num;i++){ cin>>interger[i]; } sort(interger,interger+num); while(true){ if(sum+interger[m]>length||counter==num) break; sum+=interger[m]; counter++; m++; } cout<<counter<<endl; return 0; }
1.4 算法时间及空间复杂度分析:
整体算法上看,输入需要O(n)的时间进行输入,最快用O(nlogn)的时间复杂度进行排序,使用O(n)的时间进行结果叠加,总时间复杂度为O(nlogn),时间复杂度花费在排序上。
空间上,只需要一个临时变量存储当前占用容量总和即可。
二、PTA实验报告题2 : 删数问题
2.1 实践题目:
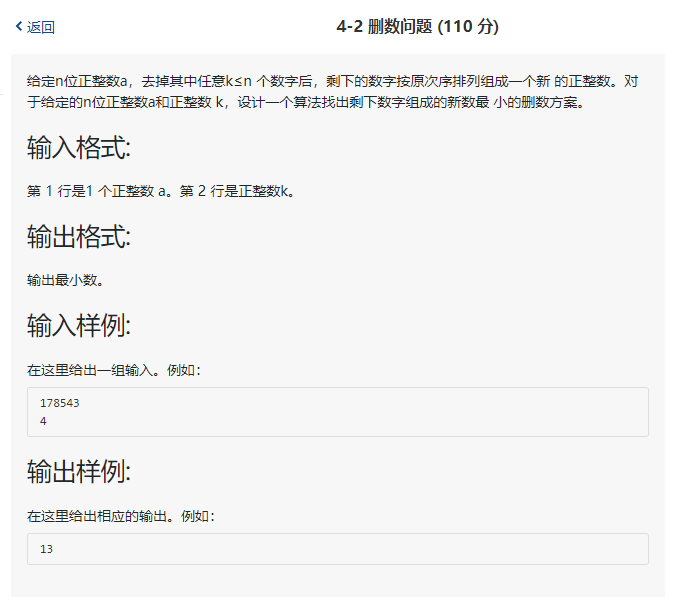
2.2 问题描述:
第二题题意是指,在给定的数字串以及可删数个数的条件下,删数指定k个数,得到的数是最小的。
2.3 算法描述:
首先,分析题目,删数问题,可以用一个比较方便的函数,String类的erase函数,这个函数可以删除字符串内的单个或多个字符,可以比较方便的处理删数问题。
第二,我们注意到这道题有个坑点,那就是前导零,我们需要注意100000,删除1后结果应为0
第三,确定我们的贪心策略:当当前的数,比后一位数大时,删去当前的数。
如:样例178543

用一个index时刻从头往后扫,不满足就后移。
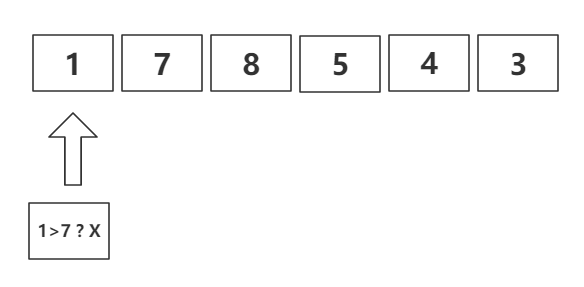
当满足之后,删除当前的值。

得到17543,这时将index重新置0,并记录已删数+1,直到满足最大删数。以此类推,直接输出string便是结果。
AC代码:
#include<iostream> #include<algorithm> #include<string> using namespace std; #define MAXLENGTH 1005 int main(){ int k; string a; cin>>a>>k; int len = a.size(); while(k>0){ for(int i = 0;(i<a.size()-1);i++){ if(a[i]>a[i+1]) { a.erase(i,1); break; } } k--; } while(a.size()>1&&a[0]=='0'){ a.erase(0,1); } cout<<a<<endl; return 0; }
2.4 算法时间及空间复杂度分析:
时间复杂度为O(n^2),即开销在不断的删数和回溯到字符串头的过程。
空间复杂度需要一个String字符串长度,因此空间复杂度是O(n)
三、PTA实验报告题3 : 最优合并问题
3.1 实践题目:

3.2 问题描述:
该题目为:题目用 2 路合并算法将这k 个序列合并成一个序列,并且合并 2 个长度分别为m和n的序列需要m+n-1 次比较,输出某段合并的最大比较次数和最小比较次数。
3.3 算法描述:
这道题算是哈夫曼算法的一道裸题,很容易解决,只需要使用优秀队列不断维护最小值或最大值即可。
哈夫曼树:是一颗最优二叉树。给定n个权值作为n个叶子的结点,构造一棵二叉树,若树的带权路径长度达到最小,这棵树则被称为哈夫曼树。
因此本题根据哈夫曼算法,我们以最小比较次数为例:
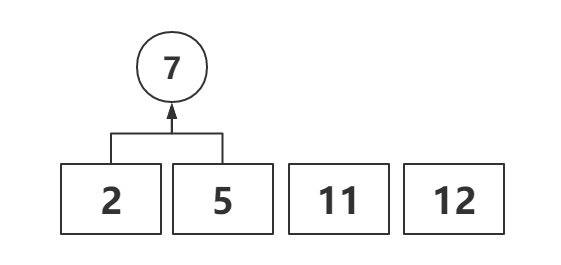
首先从队列中选出两个最小的数进行合并,并在队列中删除这两个数,并将新合成数加入队列中。
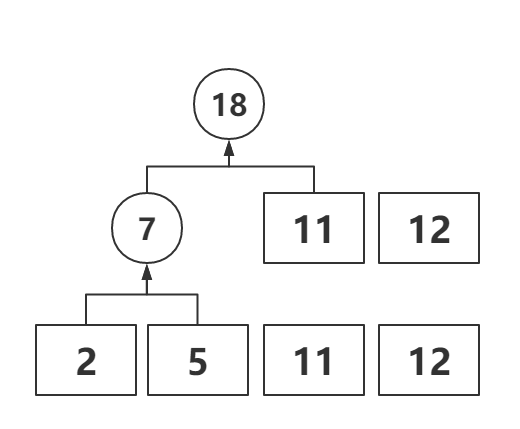
再取最小的两个数再进行合并,以此类推,得到最终的大数如下
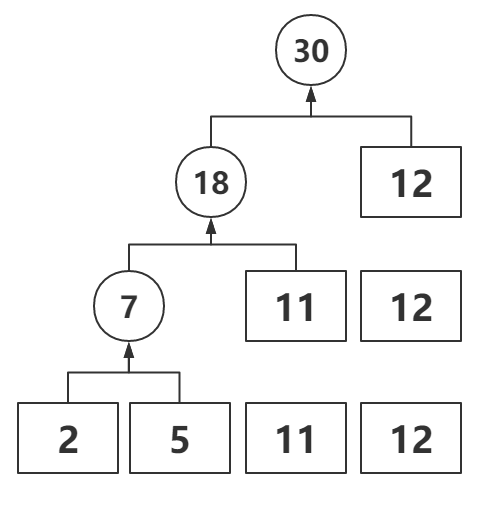
因此最小比较次数为:( 7 - 1 ) + ( 18 - 1 ) + ( 30 - 1 ) = 52,即为所得。最大比较次数也是同理。
AC代码如下:
#include<bits/stdc++.h> using namespace std; priority_queue<int> Haff; priority_queue<int, vector<int>, greater<int> > Haff2; int n,ans1,ans2; int main() { cin>>n; for(int i = 0;i<n;i++) { int temp; cin>>temp; Haff.push(temp); Haff2.push(temp); } while(1) { if(Haff.size() == 1) break; int temp1 = Haff.top(); Haff.pop(); int temp2 = Haff.top(); Haff.pop(); Haff.push(temp1+temp2); ans1 += temp1+temp2-1; } while(1) { if(Haff2.size() == 1) break; int temp1 = Haff2.top(); Haff2.pop(); int temp2 = Haff2.top(); Haff2.pop(); Haff2.push(temp1+temp2); ans2 += temp1+temp2-1; } cout<<ans1<<" "<<ans2; return 0; }
3.4 算法时间及空间复杂度分析:
由分析易知,虽然进行了两次优先队列维护,但是总的时间复杂度数量级是不变的,用O(n/2)的时间pop和push合成树。在优先队列里面用红黑树对顺序进行维护,时间复杂度为O(nlogn),最后将统计的结果输出,总的时间复杂度为O(nlogn)。
空间复杂度为两棵红黑树,即T(2n) = O(n)。
四、实验心得体会(实践收获及疑惑):
经过动态规划的肆虐之后,贪心算法变得稍微容易很多,和三木小哥哥的合作很愉快,能够很好较快及时的解决三道实践问题,暂无太多的问题,继续加油。
如有错误不当之处,烦请指正。