图的基本概念
图的定义
图是由顶点集合V和边集合E组成的。分为有向图和无向图。
图的基本术语
- 邻接
- 顶点的度、入度、出度
- 路径和路径长度
- 自回路和多重图
- 完全图
- 子图(注:图的子图必须首先满足图的定义)
- 连通图和连通分量
- 生成树
- 有向树和生成森林
- 权和网
图的类型定义
有向图的抽象数据类型定义
ADT Graph{
数据:
顶点的有限非空顶点集合V和边集合E,每条边由顶点的偶对<u,v>表示。数据元素之间的关系是多对多的关系。
运算:
Init(G,n):初始化运算。构造一个包含n个顶点没有边的图G。若构建成功,返回OK;否则,返回ERROR。
Destroy(G):撤销运算。撤销一个图G。
Exist(G,u,v):边的搜索运算。若图G中存在边<u,v>,则返回OK,否则返回Error。
Insert(G,u,v,w):边的插入运算。向图G中添加权为w的边<u,v>,若插入成功,返回OK;若图中已存在边<u,v>,则返回Duplicate;其他均返回ERROR。
Remove(G,u,v):边的删除运算。从图G中删除边<u,v>,若不存在则返回NotPresent;若存则则删除此边,返回OK;其他均返回Error。
}
图的存储结构和遍历
邻接矩阵表示法
如果u和v之间存在边,则在无向图或有向图对应的邻接矩阵中相应位置定义为1,否则定义为0。如果是带权图,则应标明权值,其他为∞。
邻接矩阵的实现、深度遍历和宽度遍历
#include <stdio.h> #define MaxVex 100 //最大顶点数 #define INFINITY 65535 //表示∞ #define TRUE 1 #define FALSE 0 typedef char VertexType; //顶点类型 typedef int EdgeType; //权值类型 typedef int Bool; Bool visited[MaxVex]; typedef struct { VertexType vexs[MaxVex]; //顶点数组 EdgeType arc[MaxVex][MaxVex]; //邻接矩阵 int numVertexes, numEdges; //当前图中的结点数以及边数 }MGraph; //广度优先遍历需要的循环队列 typedef struct { int data[MaxVex]; int front, rear; }Queue; /****************************************/ //队列的相关操作 //初始化 void InitQueue(Queue *Q) { Q->front = Q->rear = 0; } //入队 void EnQueue(Queue *Q, int e) { if ((Q->rear+1)%MaxVex == Q->front) return ; Q->data[Q->rear] = e; Q->rear = (Q->rear+1)%MaxVex; } //判空 Bool QueueEmpty(Queue *Q) { if (Q->front == Q->rear) return TRUE; else return FALSE; } //出队 void DeQueue(Queue *Q, int *e) { if (Q->front == Q->rear) return ; *e = Q->data[Q->front]; Q->front = (Q->front+1)%MaxVex; } /****************************************/ //建立图的邻接矩阵 void CreateMGraph(MGraph *G) { int i, j, k, w; printf("输入顶点数和边数: "); scanf("%d%d", &G->numVertexes,&G->numEdges); fflush(stdin); printf("============================== "); printf("输入各个顶点: "); for (i=0; i<G->numVertexes; ++i) { printf("顶点%d: ",i+1); scanf("%c", &G->vexs[i]); fflush(stdin); } for (i=0; i<G->numVertexes; ++i) { for (j=0; j<G->numVertexes; ++j) G->arc[i][j] = INFINITY; } printf("============================== "); for (k=0; k<G->numEdges; ++k) { printf("输入边(vi, vj)中的下标i和j和权W: "); scanf("%d%d%d", &i,&j,&w); G->arc[i][j] = w; G->arc[j][i] = G->arc[i][j]; } } //输出 void DisMGraph(MGraph *G) { int i, j, k; k = G->numVertexes; for (i=0; i<k; ++i) { for (j=0; j<k; ++j) { printf("%5d ", G->arc[i][j]); } putchar(' '); } } /****************************************/ //图的深度优先遍历 void DFS(MGraph G, int i) { int j; visited[i] = TRUE; printf("%c ", G.vexs[i]); for (j=0; j<G.numVertexes; ++j) { if (G.arc[i][j]!=INFINITY && !visited[j]) DFS(G, j); } } void DFSTraverse(MGraph G) { int i; for (i=0; i<G.numVertexes; ++i) visited[i] = FALSE; for (i=0; i<G.numVertexes; ++i) { if (!visited[i]) DFS(G, i); } } //图的广度优先遍历 void BFSTraverse(MGraph *G) { int i, j; Queue Q; for (i=0; i<G->numVertexes; ++i) visited[i] = FALSE; InitQueue(&Q); for (i=0; i<G->numVertexes; ++i) { if (!visited[i]) { visited[i] = TRUE; printf("%c ", G->vexs[i]); EnQueue(&Q, i); while (!QueueEmpty(&Q)) { DeQueue(&Q, &i); for (j=0; j<G->numVertexes; ++j) { if (!visited[j] && G->arc[i][j]!=INFINITY) { visited[j] = TRUE; printf("%c ", G->vexs[j]); EnQueue(&Q, j); } } } } } } /****************************************/ //程序入口 int main(){ MGraph G; CreateMGraph(&G); printf(" 图的深度优先遍历为: "); DFSTraverse(G); printf(" 图的广度优先遍历为: "); BFSTraverse(&G); printf(" "); return 0; }
邻接表表示法
在邻接表中,为图的每个顶点建立一个单链表。单链表中的每个结点代表一条边,称为边结点。
使用一维指针数组存储每条单链表中第一个边结点的地址。
邻接表的实现、深度遍历和宽度遍历
/** 无向图的邻接表存储 深度优先遍历递归 广度优先遍历递归+非递归 */ #include <stdio.h> #include <string.h> #include <malloc.h> #define N 5 #define MAX 50 typedef struct A{ int adjvex; struct A* nextArc; }Arc; typedef struct node{ char data[N]; Arc* firstArc; }Node; typedef struct graph{ Node vex[MAX]; int numv; int nume; }Graph; int getIndex(Graph G,char s[]){ for(int i = 0; i < G.numv; i++){ if(strcmp(G.vex[i].data,s) == 0) return i; } return -1; } void create(Graph& G){ printf("输入顶点和弧的个数: "); scanf("%d%d",&G.numv,&G.nume); printf("输入顶点信息: "); for(int i = 0; i < G.numv; i++) scanf("%s",G.vex[i].data); ///初始化顶点数组 for(int i = 0; i < G.numv; i++) G.vex[i].firstArc = NULL; printf("输入边的信息: "); char s[N],e[N]; int u,v; for(int i = 0; i < G.nume; i++){ scanf("%s%s",s,e); u = getIndex(G,s); v = getIndex(G,e); Arc* p = (Arc*)malloc(sizeof(Arc)); p->adjvex = v; p->nextArc = NULL; p->nextArc = G.vex[u].firstArc; G.vex[u].firstArc = p; Arc* t = (Arc*)malloc(sizeof(Arc)); t->nextArc = NULL; t->adjvex = u; t->nextArc = G.vex[v].firstArc; G.vex[v].firstArc = t; } } void output(Graph G){ Arc* p; for(int i = 0; i < G.numv; i++){ p = G.vex[i].firstArc; printf("%4s",G.vex[i].data); while(p != NULL){ printf("%4s",G.vex[p->adjvex].data); p = p->nextArc; } printf(" "); } } ///深度优先遍历 (递归) int visit[2*MAX]; void dfs(Graph G,int s){ Arc* p = G.vex[s].firstArc; if(!visit[s]){ printf("%4s",G.vex[s].data); visit[s] = 1; } while(p != NULL){ if(!visit[p->adjvex]) dfs(G,p->adjvex); p = p->nextArc; } } ///广度优先遍历 (递归) ///缺点递归最大为G.numv次 int q[2*MAX],f=0,r=0; int visit_q[MAX]; void bfs(Graph G,int s){ if(!visit_q[s]){ printf("%4s",G.vex[s].data); visit_q[s] = 1; Arc* p = G.vex[s].firstArc; while(p != NULL){ if(!visit_q[p->adjvex]) q[r++] = p->adjvex; p = p->nextArc; } } while(f < r){ bfs(G,q[f++]); } } ///广度优先遍历 (非递归) int Q[2*MAX],F=0,R=0; int visit_Q[MAX]; void bfs_1(Graph G,int s){ printf("%4s",G.vex[s].data); visit_Q[s] = 1; Arc* p = G.vex[s].firstArc; while(p != NULL){ Q[R++] = p->adjvex; p = p->nextArc; } while(F < R){ int node = Q[F++]; if(!visit_Q[node]){ printf("%4s",G.vex[node].data); visit_Q[node] = 1; p = G.vex[node].firstArc; while(p != NULL){ if(!visit_Q[p->adjvex]) Q[R++] = p->adjvex; p = p->nextArc; } } } } int main(void){ Graph G; create(G); printf("输出邻接矩阵: output(G); printf("深度优先遍历(递归): "); dfs(G,0); printf(" 广度优先遍历(递归): "); bfs(G,0); printf(" 广度优先遍历(非递归): "); bfs_1(G,0); return 0; }
拓补排序
AOV网(顶点活动网):为反映整个工程之间的领先关系,使用一个有向图,顶点代表活动,图中的有向边代表活动间的领先关系。
排序步骤:
- 在图中选择一个入度为0的顶点并输出它。
- 删除此顶点及其所有的边。
- 重复步骤1.2.,直到不存在入度为0的顶点。
算法步骤:
- 利用函数Degree求出所有顶点的入度,并存入一维数组inDegree中。
- 将入度为0的顶点存入堆栈S。
- 只要堆栈S不为空,则重复以下操作:
- 将栈顶的顶点j出栈并保存在topo数组中。
- 将顶点j邻接到的每个顶点的入度减1,若发生顶点入度为0的情况,则将该顶点入栈。
- 当堆栈为空,而输出的顶点数小于图中的顶点数,说明图中存在有向回路,返回ERROR;否则返回OK,此时topo数组中包含所有顶点的序列即为拓补序列
对于有n个顶点和e条边,时间复杂度为O(n+e)。

关键路径
AOE网(活动边网络):AOE网是一个带权有向图,以顶点表示事件,有向边表示活动,边上权表示活动持续的时间。AOE网可以用来估算工程的完成时间。
解决估算问题的方法之一是关键路径算法。所谓关键路径,就是AOE网络中从开始顶点到完成顶点的最长路径。完成工程所需的最短时间是关键路径的长度,也就是关键路径上个边的权值和。关键路径上 的活动称为关键活动。
关键路径的求解步骤:
- 求解事件Vi最早发生的时间earliest(i);
- 求解事件Vi最晚发生的时间latest(i);
- 求活动ak最早的开始时间early(k):early(k)=earliest(i);
- 求活动ak最晚的开始时间late(k):late(k)=latest(i)-w(i.j);
- 若ak满足early(k)=late(k),则为关键活动。
最小代价生成树
目标就是使用n-1条边将n个顶点连接起来,且各边的权值和最小。
普里姆(Prim)算法
最小生成树的构造过程是
- T=(V',E')是正在构造中的生成树。初始状态下,V‘={v0},E’={},即生成树中只有一个顶点v0,没有边。
- 在所有u∈V',v∈V-V'的边(u,v)∈E中找一条权值最小的边,将此边并入集合T中。
- 重复2,直至V=V'。
代码:
时间复杂度为O(n²).
找道题目做做。
 、
、
克鲁斯卡尔(Kruskal)算法
设G=(V,E)是带权连通图,T=(V',E')是正在构造中的生成树,最小代价生成树的构造过程是:
- 初始状态下,T=(V,{}),即生成树包含所有顶点,但没有边。
- 从E中选择代价最小的边(u,v),若在T中加入后不会形成回路,则加入此边,否则,选择下一条代价最小的边。
- 重复2,直到生成树中有n-1条边。
时间复杂度为O(elog2e)
最短路径
1.求单源最短路径的迪杰斯特拉(Djikstra)算法
算法思想:对于带权的有向图G=(V,E),将V中的顶点分为两个集合,集合S中存放已求出最短路径的顶点,集合V-S存放尚未确定最短路径的顶点。初始状态时,集合S中只有源点v0。按各顶点到源点最短路径长度非递减的顺序逐个将V-S中的顶点加到 S中,直到源点到其他顶点的最短路径均求得为止。
借鉴http://www.360doc.cn/article/27915668_540045384.html
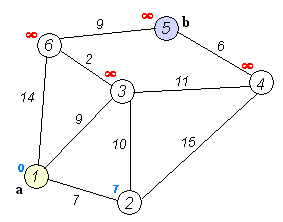
步骤如下:
- 计算出,2、3、4、5、6到原点1的距离分别为:[7, 9, -1, -1, 14]。-1表示无穷大。取其中最小的,为7,即可以确定1的最短路径为0,2为下一轮的前驱节点。同时确定2节点的最短路径为7,路线:1->2。
- 取2节点为前驱节点,按照前驱节点的最短距离加上该节点与前驱节点的距离计算新的最短距离,可以得到3,4,5,6节点到原点的距离为:[17, 22, -1, -1],此时需要将这一轮得到的结果与上一轮的比较,3节点:17 > 9,最短路径仍然为9;4节点:22 < 无穷大,刷新4节点的最短路径为22;5节点:不变,仍然为无穷大;6节点:14 < 无穷大,取14,不变。则可以得到本轮的最短距离为:[9, 22, -1, 14],取最短路径最小的节点,为3,作为下一轮的前驱节点。同时确定3节点的最短路径为9,路线:1->3。
- 同上,以3为前驱节点,得到4,5,6的计算距离为:[20, -1, 11],按照取最短路径的原则,与上一轮的进行比较,刷新为:[20, –1, 11],选定6为下一轮的前驱节点。同时取定6的最短路径为11,路线:1->3->6。
-
同上,以6为前驱节点,得到4和5的计算距离为[20, 20],与上一轮进行比较,刷新后为[20, 20],二者相等只剩下两个节点,并且二者想等,剩下的计算已经不需要了。则两个节点的最短路径都为20。整个计算结束。4的最短路径为20,路线:1->3->4。5的最短路径为20,路线:1->3->6->5。
如果二者不相等,则还需要进行第五轮,先确定二者中的一个的最短路径和路线,再取定剩下的。直到整个5次循环都完成。
算法的时间复杂度应该是O(n³)
我做道题试验试验。

2.求所有顶点之间最短路径的费洛伊德(Floyd)算法
基本思想是:递推产生n*n的矩阵序列,其中dk [i][j]表示从顶点i到顶点j的路径上所经过的顶点序号不大于k的最短路径长度。
算法的时间复杂度应该是O(n³)
借鉴https://blog.csdn.net/luo_xianming/article/details/44998227