数据处理——异常值检测

一、3σ原则

　　3σ原则又称为拉依达准则，该准则具体来说，就是先假设一组检测数据只含有随机误差，对原始数据进行计算处理得到标准差，然后按一定的概率确定一个区间，认为误差超过这个区间的就属于异常值。

　　正态分布状况下，数值分布表：

数值分布	在数据中的占比
(μ-σ,μ+σ)	0.6827
(μ-2σ,μ+2σ)	0.9545
(μ-3σ,μ+3σ)	0.9973

　　注：在正态分布中σ代表标准差,μ代表均值，x=μ为图形的对称轴

import pandas as pd
import numpy as np

# 定义3σ法则识别异常值函数
def three_sigma(Ser1):
    '''
    Ser1：表示传入DataFrame的某一列。
    '''
    rule = (Ser1.mean()-3*Ser1.std()>Ser1) | (Ser1.mean()+3*Ser1.std()< Ser1)
    index = np.arange(Ser1.shape[0])[rule]
    outrange = Ser1.iloc[index]
    return outrange

# 导入数据并调用three_sigma
df = pd.read_csv('./data.csv',encoding= 'gbk')
three_sigma(df['counts']).head()

　　

二、箱线图检测异常值

　　和3σ原则相比，箱线图依据实际数据绘制，真实、直观地表现出了数据分布的本来面貌，且没有对数据作任何限制性要求（3σ原则要求数据服从正态分布或近似服从正态分布），其判断异常值的标准以四分位数和四分位距为基础。四分位数给出了数据分布的中心、散布和形状的某种指示，具有一定的鲁棒性，即25%的数据可以变得任意远而不会很大地扰动四分位数，所以异常值通常不能对这个标准施加影响。鉴于此，箱线图识别异常值的结果比较客观，因此在识别异常值方面具有一定的优越性。

　　箱型图提供了识别异常值的一个标准，即异常值通常被定义为小于QL-1.5IQR或大于QU+1.5IQR的值。其中，QL称为下四分位数，表示全部观察值中有四分之一的数据取值比它小；QU称为上四分位数，表示全部观察值中有四分之一的数据取值比它大；IQR称为四分位数间距，是上四分位数QU与下四分位数QL之差，其间包含了全部观察值的一半。

# 定义箱线图识别异常值函数
def box_plot(Ser):
    '''
    Ser：进行异常值分析的DataFrame的某一列
    '''
    Low = Ser.quantile(0.25)-1.5*(Ser.quantile(0.75)-Ser.quantile(0.25))
    Up = Ser.quantile(0.75)+1.5*(Ser.quantile(0.75)-Ser.quantile(0.25))
    index = (Ser< Low) | (Ser>Up)
    Outlier = Ser.loc[index]
    return(Outlier)

# 调用
box_plot(df['counts']).head(8)

　　

　　

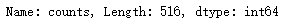
　　或许我们还可以统计Ser中的非空值个数：

def box_plot_null(Ser):
    '''
    Ser：进行异常值分析的DataFrame的某一列
    函数将Ser中的异常值赋值None
    '''
    Low = Ser.quantile(0.25)-1.5*(Ser.quantile(0.75)-Ser.quantile(0.25))
    Up = Ser.quantile(0.75)+1.5*(Ser.quantile(0.75)-Ser.quantile(0.25))
    index = (Ser< Low) | (Ser>Up)
    Ser.loc[index] = None
    return(Ser)

box_plot_null(df['counts']).notnull().sum()