遍历的含义:
在二叉树的一些应用中,常常要求在书中查找具有某种特征的结点,或者对书中全部结点逐一进行某种处理。这就引入了遍历二叉树的问题
遍历二叉树:指某种次序访问二叉树上所有结点,使每个结点呗访问依次且仅被访问一次。
遍历规则:
由二叉树的递归定义知,二叉树的三个基本组成是:根节点,左子树,右子树
L:遍历左子树
D:访问根节点
R:遍历右子树
组合为: LDR 、LRD 、DLR
RDL 、RLD 、DLR
DLR :先(根)序遍历
LDR:中(根)序遍历
LRD:后(根)序遍历,
先序遍历 DLR:
首先访问根结点,其次遍历根结点左边的左子树,最后遍历根结点右边的右子树,每一颗子树都要(先根、再左,后右)
中序遍历 LDR:
首先遍历根结点的左子树,其次访问根结点,最后遍历根结点的右子树,每一棵子树都要按照(先左,再根,后右)
后序遍历 LRD:
首先遍历根结点的左子树,其次遍历根结点的右子树,最后访问根结点,每一颗子树都要按照同样顺序(先左,再右,后根)
遍历算法:
1、先序遍历:
步骤:若二叉树为空,则执行空
否则:(1)访问根结点
(2)先序遍历左子树
(3)先序遍历右子树
算法:
1 void preorder(Bintree bt){ 2 if(bt!=NULL)//先序遍历以bt为根的二叉树 3 visit(bt); 4 preorder(bt->lchild); 5 preorder(bt->rchild); 6 }
2、中序遍历
步骤: 若二叉树为空,执行空操作;
否则: (1)中序遍历左子树;
(2)访问根结点;
(3)中序遍历右子树。
1 void inorder(Bintree bt){ 2 if(bt!=NULL){ 3 inorder(bt->Ichild); 4 visit(bt); 5 inorder(bt->rchild); 6 }}
3、后序遍历
若二叉树为空,则退出;
否则: (1)后序遍历根的左子树;
(2)后序遍历根的右子树。
(3)访问根结点
void postorder (Bintree bt ) { if (bt! =NULL){ postorder ( bt->lchild ) ; postorder ( bt->rchild ) ; visit(bt);} }
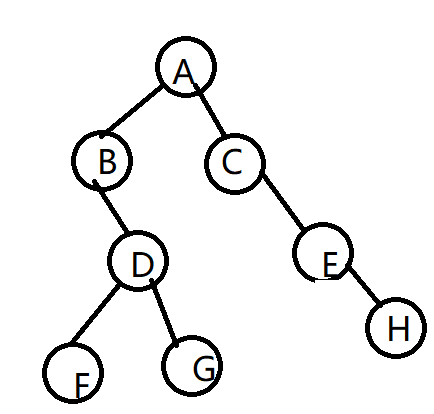
根据图可以进行遍历
先序遍历:(根左右)A-B-D-F-G-C-E-H
中序遍历:(左根右)B-F-D-G-A-C-E-H
后序遍历:(左右根)B-F-G-D-H-E-C-A
任意一棵二叉树的前序和后序遍历的结构序列中,个叶子结点之间的相对次序关系都相同
若只给出中序和后序该如何建立二叉树呢?
中序B-A-C-D-E-F-G-H
后序B-C-A-E-D-G-H-F
---------------------------------------------------------------
通过两个序列,可以先看出根结点为F,
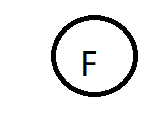
中序是左根右
后序是左右根
所以将右子树的G H找到,因为后序是左右根,所以 G在H上
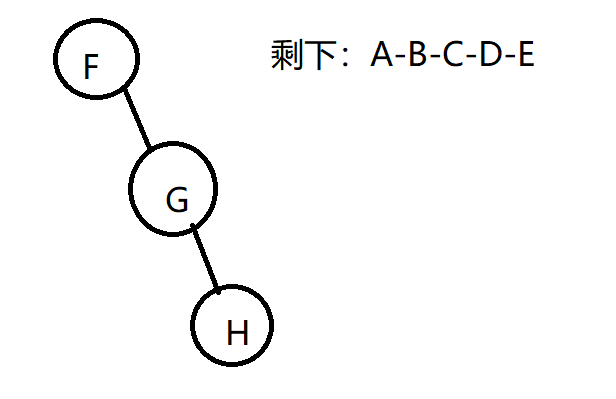
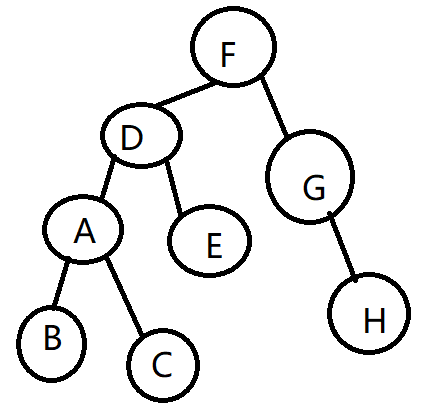
两个中B在最左边所以最下面有一个B,接着再看后序B-C-A-E-D-G-H-F ,得出C在B的右边 ,B-C的根是A,中序B-A-C-D-E-F-G-H中验证A是B-C的根,再看后序的A-E-D是左右根,所以D是A-E的根,
编写求二叉树中叶结点个数的算法(设二
叉树的二叉链表的根指针为bt)
1 int leafcount (Bintree bt ) { 2 /*求二叉树bt中叶结点的数目*/ 3 if ( bt == NULL ) return (0) ; 4 else 5 if ( bt->lchild == NULL && bt->rchild == NULL ) 6 return (1) ; 7 else { 8 n = leafcount( bt->lchild ) ; /* 求左子树的叶子数目*/ 9 m = leafcount(bt->rchild) ; /* 求右子树的叶子数目*/ 10 return (m+n) ; 11 } 12 }
编写输出二叉树中所有度为1的结点的数据域的
值,并统计其数目的算法(设二叉树的二叉链表的根指
针为t)
int onesoncount(Bintree t) /*输出二叉树t中度为1的结点值,并求其个数*/ { if (t==NULL) return(0); else if ((t->lchild==NULL && t->rchild!=NULL) || (t->lchild!=NULL && t->rchild==NULL)) { printf(t->data); return(onesoncount(t->lchild)+ onesoncount(t->rchild)+1); } else return(onesoncount(t->lchild)+ onesoncount(t->rchild)); }
编写输出二叉树中所有度为2的结点的数据域的
值,并统计其数目的算法(设二叉树的二叉链表的根指
针为BT)
int twoson(Bintree BT) /*输出二叉树BT中所有度为2的结点的数据域值,并统计其数目*/ { if (BT==NULL) return(0); else if (BT->lchild==NULL || BT->rchild==NULL) return(twoson(BT->lchild)+ twoson (BT->rchild)); else if (BT->lchild!=NULL && BT->rchild!=NULL) { printf(BT->data); return(twoson(BT->lchild)+ twoson(BT->rchild)+1); } }
编写一算法,打印出一棵二叉树中所有非终端
结点的值,并统计非终端结点的个数。 (二叉树以二叉
链表存储,根指针为bt)
int notleafcount (Bintree bt ) /*求二叉树bt中非叶结点的数目*/ { if ( bt = = NULL ) return (0) ; else if ( bt->lchild = = NULL && bt->rchild = = NULL ) return (0) ; /*无左右子树*/ else { printf(bt->data); /* 输出非终端结点值*/ n = notleafcount( bt->lchild ) ; /* 求左子树的非终端结点数目*/ m = notleafcount(bt->rchild) ; return (m+n+1) ; /* 返回总的非终端结点数*/ } }
编写一算法,打印出一棵二叉树中所有结点的
值,并统计结点的个数。 (二叉树以二叉链表存储,根
指针为bt)
int f5 (Bintree bt )
/* 打印出二叉树t中所有结点的值,并统计结点的个数 */
{ if ( bt == NULL )
return (0) ;
else
{ printf(bt->data); /* 输出结点值*/
n = f5( bt->lchild); /* 求左子树的结点数目*/
m = f5( bt->rchild); /* 求右子树的结点数目*/
return (m+n+1) ; /* 返回总的结点数*/
}
}
设二叉树存储结构采用二叉链表表示,每个结
点的数据域中存放一个整数。试编写一个算法,求此
二叉树上数据域的值为8的结点个数。
int f6 (Bintree bt ) /*求二叉树bt结点数据域值为8的结点的数目*/ { if ( bt == NULL ) return (0) ; else if (bt->data=8) return(f6(bt->lchild)+f6(bt->rchild)+1); else return(f6(bt->lchild)+f6(bt->rchild)); }