树的存储结构
一、双亲表示法
以一组连续空间存储树的结点,即一个一维数组构成,数组每个分量包含两个域,数据域和双亲域。数据域用于存储树上一个结点的数据元素值,双亲域用于存储本结点的双亲结点在数组中的序号(下标值)
 它的双亲表示法
它的双亲表示法
A为根结点没有双亲所以它的双亲值是-1,B,C是A的子节点,所以它们的双亲为0;
1 #define size 10 2 typedf struct { 3 datatype data; 4 int parent; 5 }Node; 6 Node slist[size];
二、孩子链表表示法
# define MAXND 20 typedef struct bnode {int child; struct bnode *next; }node,*childlink; Typedef struct { DataType data; childlink hp; }headnode; Headnode ; link[MAXND];
在孩子链表表示中,找孩子方便,但 求
结点的双亲困难,因此可在顺序表中再增加
一个域,用于指明每个结点的双亲在表中位
置,即将双亲表示法和孩子链表表示法结合
起来。
双亲孩子表示法
树中每个结点的孩子串成一单链表 孩子链表 N个结点——n个孩子
同时用一维数组顺序存储树中各结点,数组元素除了包括结点本身的信息和该结点的孩子链表的头指针之外,还增设一个域,用来存储结点双亲结点在数组中的序号。
三、孩子兄弟链表表示法
结点形式:son data brother
son:指结点的第一个孩子结点,
brother:指结点的下一个兄弟结点
Typedef struct tnode{ Data TYpe data; struct tnode *son,*borther; }*Tree;
一般树转化二叉树
方法:1)各兄弟之间加连线
2)对任一结点,除最左孩子外,抹掉该结点与其余孩子的各枝
3)以根为轴心,将连线顺时针转45度
森林转化二叉树
方法:1)将每颗树转换成相应的二叉树
2)将1)中的各棵二叉树的根结点看作是兄弟连接起来
二叉树还原成一般树:
1)从根结点起
2)该结点左孩和左孩右枝上的结点一次作为该结点孩子;
3)重付1
树和森林的遍历
一、树的遍历
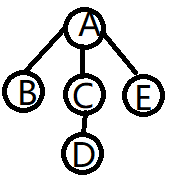
先序遍历:先访问根结点,然后依次先序遍历根的每颗子树
ABCDE
后序遍历:先依次后序遍历每颗子树,最后访问根结点
BCDEA
层次遍历 ABCED
二、森林的遍历
先序遍历森林:访问森林中每棵树的根结点;先序遍历森林中第一颗树的根结点的子树组成的森林;先序遍历除去第一棵树之外其余的树组成的森林
中序遍历森林:中序访问森林中第一颗树的根结点的子树组成的森林;访问第一颗树的根结点;中序遍历除去第一棵树之外其余的树组成的森林;
判定树和哈夫曼树
判定树:用于描述分类过程中的二叉树,其中:每个非终端结点包含一个条件,对应依次比较;每个终端结点包含一个种类标记,对应于一种分类结果。
对n个树分类花费时间较多。因为大多数元素属于中和良,这样大多数数据都得通过3至4次判断,这样总的判断次数就多。
一、路径长度
叶结点带权的二叉树:
一组实数{p1,p2,p3,p4,.....,pk},每个叶子{n1,n,2,n3,n4,....,nk}
结点ni的带权路径长度:
为结点ni到树根的路径长度*结点ni所带的权
叶结点带权的二叉树路径长度WPL:

其中:n——叶子树
pk——第k个叶子的权
lk——从根到第k个叶子的路径长度(分支数)
哈夫曼算法:
方法:给定N个权值{p1,p2,p3....,pn}{n个叶子带的权}
构造: 森林F'={T1,T2,...,Tn},
1)取F中T1和T2(权最小的二棵)生成一颗二叉树T,T为根,t1,t2,分别为t的左、右子树
T的权=T1的权+T1的权
2)T插入到F的余下森林中(按序)
重复1、2,直到F={T}为二叉树,此二叉树T为哈夫曼树