之前咱们讲过集合、树形那么图到底是什么样子呢?

看着和树很像吧,其实图是在树的基础上的延伸,接下来看一下图的定义
图的定义:
图G:是由顶点V和边E组成的,记作:G=(V,E) 其中V是顶点集(非空)E是边集(可空)
边是顶点的有序对或无序对。(边反映了两顶点之间的关系)

可以看一下按照定义来说上图那些可以称为图呢?
a 没有顶点没有边不是,
b由顶点有边是
c有顶点有边是
c有顶点有边是
d没有顶点有边不是
有向图:边是顶点的有序对的图。

V(G)={1,2,3}
E(G)={<1,2>,<2,1>,<2,3>}
无向图:边是顶点的无序对的图。
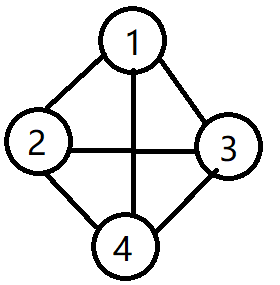
V(G1)={1,2,3,4}
E(G1)={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}
注:1)边集可空
2)边集中不允许出现相同的边
图的基本术语
顶点Vertex:图中的数据元素
<Vi ,Vj> :有向图中,顶点Vi 到Vj的边,也称弧
<弧头 终端点:箭头端
>弧尾 初始点:无箭头端
完全图:1)无向完全图 :边数=n*(n-1)/2的无向图
2)有向完全图:边数=n*(n-1)的有向图
权:与同住的边相关的数;
子图:若图G和G',有V(G)属于V(G)和E(G')属于E(G),则称G‘为图G的子图
邻接:若(Vi,Vj)∈E(G),则称Vi和Vj互为邻接点;
关联: 若(Vi,Vj)∈E(G),则称边(Vi,Vj)关联于顶点Vi和Vj;
注: 1)邻接是指顶点之间的关系,而关联是指边与顶点间的关系。
2) 若弧<Vi,Vj>∈E(G), 则称Vj是Vi的邻接点
度:无向图:顶点Vi的度为与Vi相关联的边的个数; D(V1)
有向图 :1)出度:顶点Vi的出度为以Vi为尾的出边数;OD(V1)
2)入度:顶点Vi的入度为以Vi为头的入边数; ID(V1)
3)度:有向图的度=入度+出度; DV(V1)=OD(V1)+ID(V1)
路径:图中,顶点Vp至顶点Vq的路径是顶点序列
{ Vp,Vi1,Vi2,…,Vin,Vq } 且
对无向图,边(Vp,Vi1),(Vi1,Vi2),…,(Vin,Vq)∈VR(G);
对有向图,弧<Vp,Vi1>,<Vi1,Vi2>,…,<Vin,Vq>∈VR(G);
路径长度:路径上边或弧的数目;
简单路径:除第一个和最后一个外,其余各顶点均不
相同的路径;
回路:第一个和最后一个顶点相同的路径,也称环;
简单回路:第一个和最后一个顶点相同的简单路径;
注:回路中可以有多个圈,而简单回路只能有一个圈。
连通:无向图中,若从顶点Vi到Vj顶点有路径,则
称Vi和Vj是连通的。

生成树: 含有该连通图的全部顶点的一个极小连通子图。
若连通图G的顶点个数为n,则G的生成树的边数为n-1。
G的子图G’边数大于n-1,则G’中一定有环。
G的子图G’边数小于n-1,则G’中一定不连通。
生成森林:在非连通图中,每个连通分量都可得到一个极小
连通子图,也就是生成树。这些生成树就组成了一个非连通图
的生成森林。