题目链接
https://leetcode-cn.com/problems/happy-number/
题目描述
编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」定义为:对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和,然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。如果 可以变为 1,那么这个数就是快乐数。
如果 n 是快乐数就返回 True ;不是,则返回 False 。
示例: 输入:19 输出:true 解释: 12 + 92 = 82 82 + 22 = 68 62 + 82 = 100 12 + 02 + 02 = 1
解题思路
1.无论如何,都需要求解数n每一位的平方和(求解数字的每一位值是有模板的,只需要一个while循环即可搞定)。
2.题目中说到经过变换的数字最终只有两种结果:变为1以及无限循环。对于最终变为1的情况很好处理,所以主要考虑经过处理后的数据变为无限循环的情况。
经过分析,题目就变为如何处理经过处理后的数据变为无限循环的情况(以数字116为例)。
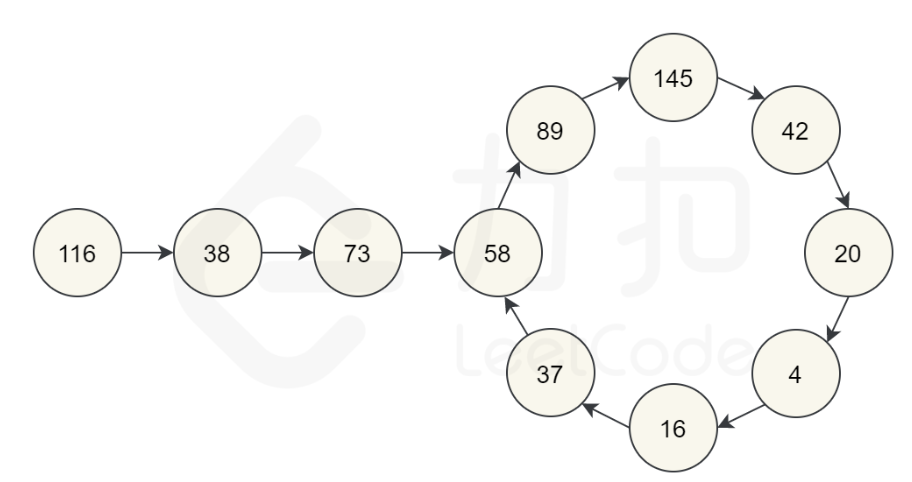
- 可以利用结合set判断数据是否出现重复,如果是,则说明进入死循环。
- 借鉴链表判断是否出现环的原理,利用快慢指针判断是否因为出现数字1而进入无限循环。
AC代码
1.采用set进行判断是否出现重复。
1 class Solution { 2 public: 3 int cal(int n) 4 { 5 int sum = 0; 6 while(n) //3行代码搞定求解数字n的每一位值 7 { 8 sum += (n % 10)*(n % 10); 9 n = n / 10; 10 } 11 return sum; 12 } 13 bool isHappy(int n) { 14 set<int> st; 15 st.insert(n); 16 while(true) 17 { 18 n = cal(n); 19 if(n == 1) return true; 20 if(st.count(n)) return false; 21 else st.insert(n); 22 } 23 24 } 25 };
2.采用快慢指针
1 class Solution { 2 public: 3 int cal(int n) 4 { 5 int sum = 0; 6 while(n) 7 { 8 sum += (n % 10) * (n % 10); 9 n = n / 10; 10 } 11 return sum; 12 } 13 bool isHappy(int n) { 14 int fast = n; 15 int slow = n; 16 while(true) 17 { //快慢指针,slow走一步,fast走两步。 18 slow = cal(slow); 19 fast = cal(fast); 20 fast = cal(fast); 21 if(slow == fast) break; 22 } 23 // if(slow == 1) return true; 24 // else return false; 25 return slow == 1;//判断是否是因为数字1而进入死循环,如果是则返回true, 26 27 } 28 };