题目链接
https://leetcode-cn.com/problems/longest-increasing-path-in-a-matrix/
题目描述
给定一个整数矩阵,找出最长递增路径的长度。
对于每个单元格,你可以往上,下,左,右四个方向移动。 你不能在对角线方向上移动或移动到边界外(即不允许环绕)。
示例 1: 输入: nums = [ [9,9,4], [6,6,8], [2,1,1] ] 输出: 4 解释: 最长递增路径为 [1, 2, 6, 9]。
示例 2: 输入: nums = [ [3,4,5], [3,2,6], [2,2,1] ] 输出: 4 解释: 最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。
解题思路
DFS+记忆化搜索
这题很容易想到利用DFS进行解决,但是本题单单采用DFS是没办法解决的,必须加上记忆化搜索。那什么是记忆化搜索呢?看看以下的问题,你就能明白什么情况要加上记忆化搜索
Q:我们之前做过连通块的题目,该题目要求你算出一共有多少个连通块,如果将题目更改一下,问你如何求出面积最大的连通块呢?
A:因为题目中我们肯定是需要对比多个连通块之间的面积,倘若你用一个变量去存储面积最大的连通块,该值也会因为DFS递归函数弹栈而改变,所以我们必须利用其他数据结构对值进行记录,这就是记忆化搜索,一般都是采用和地图规模一样大的二维数组。
弄清了DFS+记忆化搜索的概念,回到本题:
本题类似,每个元素都有4种状态可以选择,上下左右,然后套用递归模板即可。
注意:再写递归函数的时候,我们必须要理解这个递归函数表达的意义,否则很容易绕进去,以AC代码C++为例,f(int i,int j)该递归函数的意思表示:到matrix[i][j]这个元素的递增路径长度,所以也能理解f(aa,bb)+1中+1的含义:到matrix[aa][bb]的长度为f(aa,bb),则到下一个满足条件的元素的递增路径长度当然是在此基础上+1.
AC代码
C++版本
class Solution { public: vector<vector<int>> dp; vector<vector<int>> data; int dx[4] = {-1, 1, 0, 0}; int dy[4] = {0, 0, -1, 1}; int ans = 0; int n, m; int f(int i, int j) { // cout << i << " " << j << endl;
//递归必须要有出口和剪枝
//if就是递归的剪枝 if (dp[i][j]) return dp[i][j]; else { dp[i][j] = 1; for (int k = 0; k < 4; k ++) { int aa = i + dx[k], bb = j + dy[k]; if (aa < 0 || aa >= n || bb < 0 || bb >= m) continue; if (data[aa][bb] > data[i][j]) dp[i][j] = max(dp[i][j], f(aa, bb) + 1);//当递归返回值不是void的时候,通常递归表达式都需要做+或者其他运算,例如本题f(aa,bb)+1 } ans = max(ans, dp[i][j]); cout<<"i:"<<i<<",j:"<<j<<endl; //方便理解递归 cout<<dp[i][j]<<endl; return dp[i][j]; } } int longestIncreasingPath(vector<vector<int>>& matrix) { n = matrix.size(); data = matrix; if (n == 0) return 0; m = matrix[0].size(); dp = vector<vector<int>>(n, vector<int>(m, 0)); for (int i = 0; i < n; i ++) { for (int j = 0; j < m; j ++) { if (dp[i][j] == 0) f(i, j); ans = max(ans, dp[i][j]); } } return ans; } };
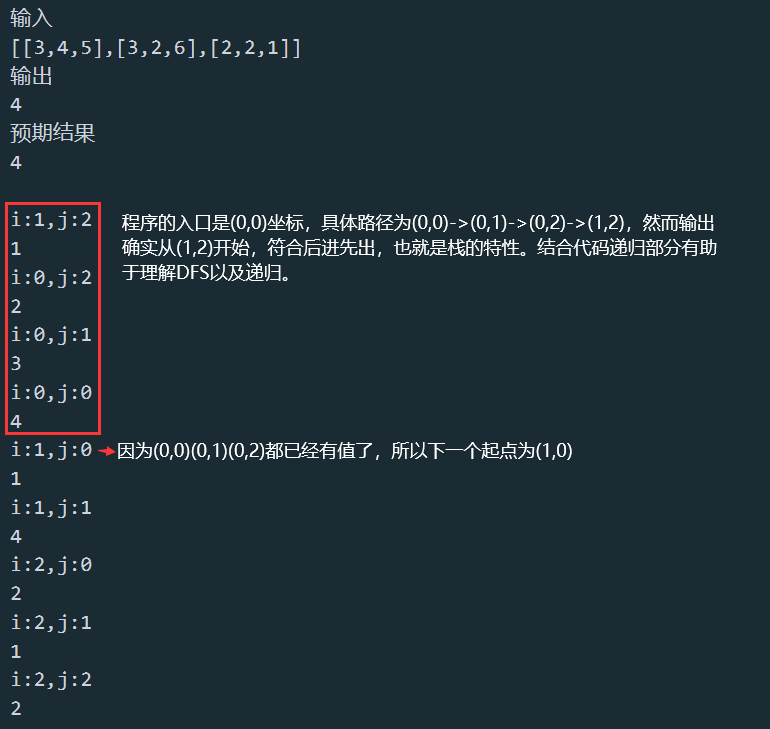
以示例2为例子,在源代码中添加两个cout语句,方便理解递归。
示例 2: 输入: nums = [ [3,4,5], [3,2,6], [2,2,1] ] 输出: 4
Java版本
class Solution { int[][] dir = {{0,1},{0,-1},{1,0},{-1,0}}; int ans = 0; public int dfs(int[][] matrix,int x,int y,int[][] dp){ //递归必须要有出口和剪枝 if(dp[x][y] != 0) return dp[x][y]; else { dp[x][y] = 1; for(int i = 0; i < 4; i++){ int xx = x + dir[i][0]; int yy = y + dir[i][1]; if(test(matrix,xx,yy) == false) continue; if(matrix[xx][yy] > matrix[x][y]){ dp[x][y] = Math.max(dp[x][y], dfs(matrix,xx,yy,dp) + 1); } } ans = Math.max(ans,dp[x][y]); return dp[x][y]; } } public boolean test(int[][] matrix,int x,int y){ if(x < 0 || x >= matrix.length) return false; if(y < 0 || y >= matrix[0].length) return false; return true; } public int longestIncreasingPath(int[][] matrix) { if(matrix.length == 0 || matrix[0].length == 0) return 0; int[][] dp = new int[matrix.length][matrix[0].length]; for(int i = 0; i < matrix.length; i++){ for(int j = 0; j < matrix[0].length; j++){ dfs(matrix,i,j,dp); } } return ans; } }