题目描述
全排列计算,计算12345的所有全排列情况
解题思路
1.回溯法
说白了还是利用DFS进行递归!
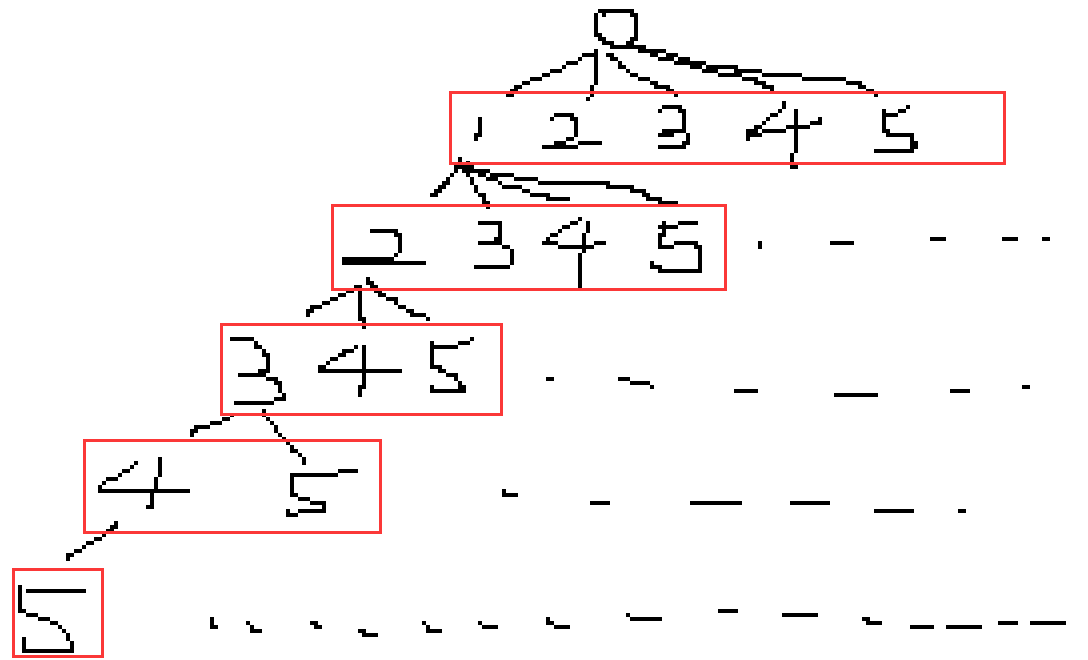
- 整棵递归树如上图所示,一共5层,每层都有1、2、3、4、5共5种取法(图中之所以后面几层没有画5种取法,是因为存在visit数组,所以省略了)因为不能重复,所以我们要用visit数组用来记录5个数字中哪些数字被访问了,哪些没有访问。
- 当遇到递归出口时,也就代表完成了一组数据,将数据打印即可。
AC代码
package test;
import java.util.*;
public class test
{
static LinkedList<Integer> ans = new LinkedList<>();
static int visit[] = new int[100];
static void dfs(int n,int num){
if(n == 0){
System.out.println(ans);
return;
}
for(int i = 1; i <= num; i++){
if(visit[i] == 0) {
visit[i] = 1;
ans.add(i);
dfs(n-1,num);
ans.removeLast();
visit[i] = 0;
}
}
}
public static void main(String[] args)
{
int n = 5;
dfs(n,n);
}
}
//可以利用数组记录答案,因为回溯的时候会把原有值覆盖,利用LinkedList动态数组花费的开销更大
package test;
import java.util.*;
import java.util.function.IntConsumer;
public class test
{
static int ans[] = new int[100];
static int visit[] = new int[100];
static void dfs(int n,int num){
if(n == 0){
for(int i = 1; i <= 5; i++) System.out.print(ans[i]);
System.out.println();
return;
}
for(int i = 1; i <= num; i++){
if(visit[i] == 0) {
visit[i] = 1;
ans[n] = i;
dfs(n-1,num);
visit[i] = 0;
}
}
}
public static void main(String[] args)
{
int n = 5;
dfs(n,n);
}
}
2.打印字符串的全部子序列
给定 "pwwkew"
子串是pww,wwk等很多个子串 是连在一起的
子序列是 pwk,pke等很多个子序列 ,但是子序列中的字符在字符串中不一定是连在一起的。
解题思路
依旧是采用回溯法,491. 递增子序列就是基于字符串全部序列的一个题目。
本题与上一题全排列的区别在于:全排列每层都有固定个数的选择,例如12345全排列,则每一层都有5中取法,而在打印字符串全部子序列中,每层的选择逐层减少一个。

AC代码
package test;
import java.util.*;
public class test
{
static LinkedList<Character> ans = new LinkedList<>();
static Set<LinkedList<Character>> sSet = new HashSet<>();//去重操作!
static void dfs(int index, String s) {
if(index > s.length()) return;
if(ans.size()!=0) {
//set中的add函数返回true证明插入成功,返回false证明已经存在该元素,插入失败
boolean flag = sSet.add(new LinkedList<>(ans));
if(flag == true) System.out.println(ans);
}
for(int i = index; i < s.length(); i++) {
ans.add(s.charAt(i));
dfs(i+1, s);//
//体现回溯思想
ans.removeLast();
}
}
public static void main(String[] args)
{
dfs(0, "abcd");
}
}
//输出
[a]
[a, b]
[a, b, c]
[a, b, c, d]
[a, b, d]
[a, c]
[a, c, d]
[a, d]
[b]
[b, c]
[b, c, d]
[b, d]
[c]
[c, d]
[d]