【LeetCode】三题解决常见异或运算题

题目一

1.1 题目链接

136. 只出现一次的数字

1.2 题目描述

1.3 解题思路

1.位运算之异或操作

异或的性质如下
(1) 两个数字异或的结果:a ^ b = 将 a 和 b 的二进制每一位进行运算，得出的数字.
(2) 运算的逻辑是:如果同一位的数字相同则为 0，不同则为 1
(3) 任何数和本身异或则为0,6 ^ 6 = 0
(4) 任何数和0异或是本身, 6 ^ 0 = 6
(5) 异或满足交换律。 即 a ^ b ^ c ，等价于 a ^ c ^ b

1.4 AC代码

class Solution {
    public int singleNumber(int[] nums) {
        int single = 0;
        for (int num : nums) {
            single ^= num;
        }
        return single;
    }
}

题目二

2.1 题目链接

剑指 Offer 56 - I. 数组中数字出现的次数

2.2 题目描述

2.3 解题思路

1.依旧是利用异或运算

异或的性质如下
(1) 两个数字异或的结果:a ^ b = 将 a 和 b 的二进制每一位进行运算，得出的数字.
(2) 运算的逻辑是:如果同一位的数字相同则为 0，不同则为 1
(3) 任何数和本身异或则为0,6 ^ 6 = 0
(4) 任何数和0异或是本身, 6 ^ 0 = 6
(5) 异或满足交换律。 即 a ^ b ^ c ，等价于 a ^ c ^ b

与题目一相比，本题难度在于得把两个不同的数字分开，分到两个组中，然后在两个组中分别利用题目一的解法即可求出答案。

核心思路：两个不同的数字的二进制表达中至少有一位不同，根据这一位不同结合&运算的结果即可把两个数字分开，因为其余数字都是两两相同，所以相同的数字必然是分到同一组中。我们只需要找出那位不同的数字mask，即可完成分组（ & mask ）操作。

num1:       101110
num2:       111110
num1^num2:  010000

可行的mask:  010000 

num1&mask = 000000
num2&mask = 010000
这样就成功把两个不同的数字分为两组，

2.4 AC代码

class Solution {
    public int[] singleNumbers(int[] nums) {
        int mask = 0;
        int[] ans = new int[2];
        int ans1 = 0;
        int ans2 = 0;
        for(int i = 0; i < nums.length; i++){
            mask = mask ^ nums[i];
        }
        int bit = 0;
        while(true){
            int a = mask & 1;
            if(a == 1){
                mask = (int)Math.pow(2,bit);
                break;
            }
            mask = mask >> 1;
            bit++;
        }
        for(int i = 0; i < nums.length; i++){
            int a = nums[i] & mask;
            if(a == 0){
                ans1 = ans1 ^ nums[i];
            }else{
                ans2 = ans2 ^ nums[i];
            }
        }
        ans[0] = ans1;
        ans[1] = ans2;
        return ans;
    }
}

题目三

3.1 题目链接

剑指 Offer 56 - II. 数组中数字出现的次数 II

3.2 题目描述

3.3 解题思路

这一题就不能单纯的利用异或运算解决问题了。

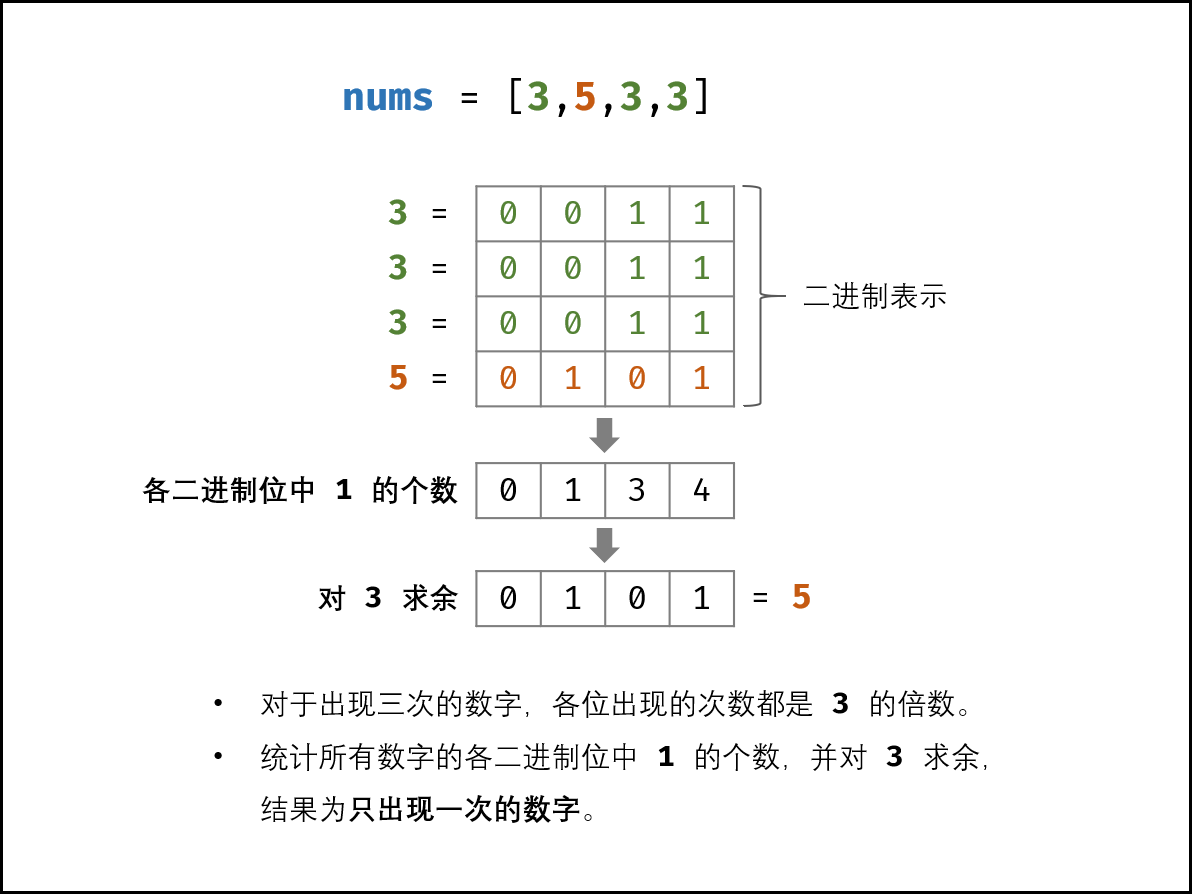
考虑数字的二进制形式，对于出现三次的数字，各 二进制位 出现的次数都是 33 的倍数。因此，统计所有数字的各二进制位中 11 的出现次数，并对 33 求余，结果则为只出现一次的数字。

3.4 AC代码

class Solution {
    public int singleNumber(int[] nums) {
        int sum[] = new int[32];
        for(int i : nums){
            int tot = 0;
            int temp = 1;
            while(tot < 32){
                int num = i & temp;
                if(num != 0) sum[tot] += 1;
                temp <<= 1;
                tot++;
            }
        }
        int ans = 0;
        for(int i = 0; i < 32; i++){
            if(sum[i] % 3 == 0){
                sum[i] = 0;
            }else{
                sum[i] = 1;
                ans += (int)Math.pow(2,i);
            }
        }
        return ans;
    }
}