问题描述
同志们,你们有没有遇到过这样的一个问题,当你在控制台上面敲入0.1+0.2这段代码的时候,惊讶的发现竟然不等于0.3

这真是惊呆我了,为什么JavaScript还有这种“骚”操作?

这种送分题,js却送了命。令人窒息的操作。这个例子很常见,我们不是为了关注这个例子本身,我们需要明白的是为什么会出现这样的结果?哪一步出了问题?还有那些计算可能会出现这样的问题?怎么解决?
看一下JavaScript是如何表示数字的?
JavaScript使用Number类型表示数字(整数和浮点数),遵循 IEEE 754 标准 通过64位来表示一个数字
通过图片具体看一下数字在内存中的表示
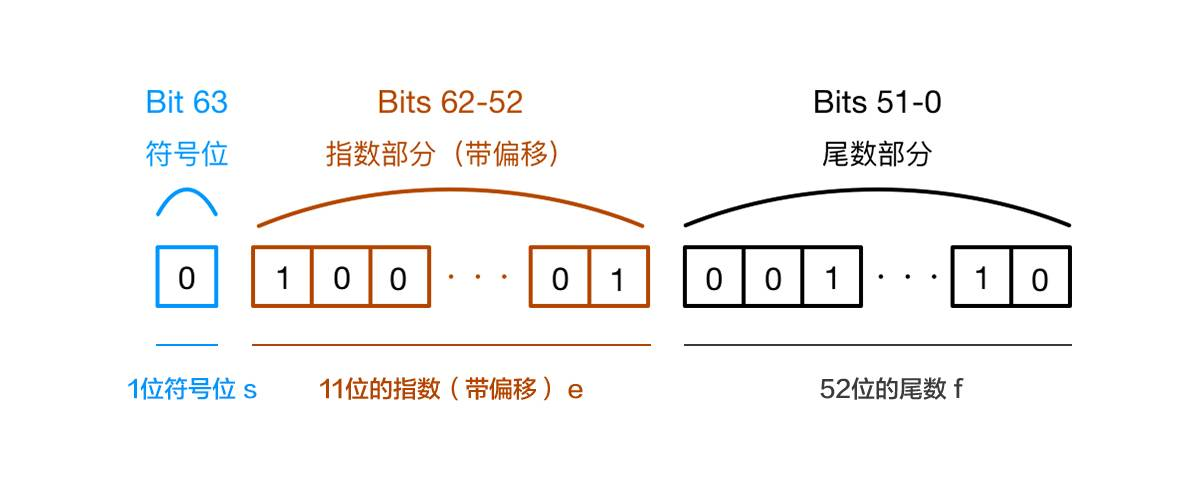
图片文字说明
- 第0位:符号位,0表示正数,1表示负数(s)
- 第1位到第11位:储存指数部分(e)
- 第12位到第63位:储存小数部分(即有效数字)f
简单验证一下:
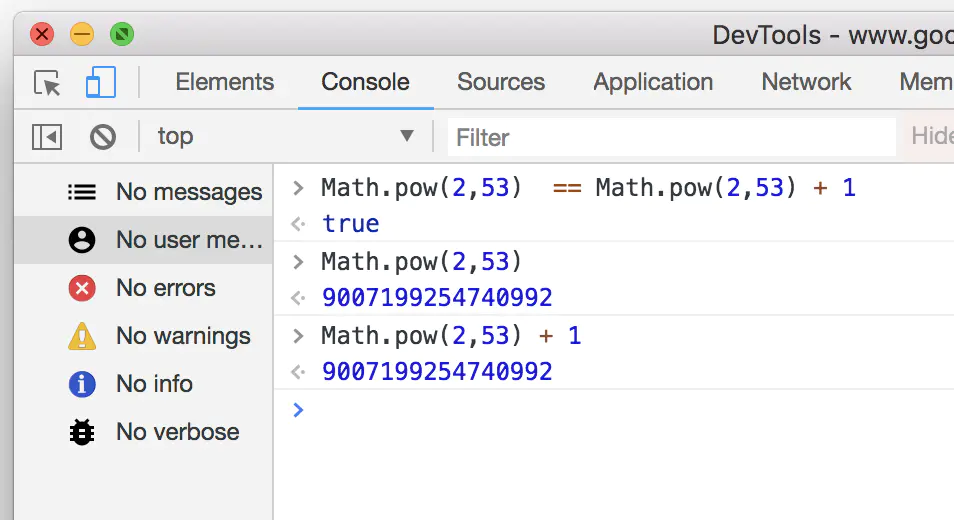
运算时发生了什么?
首先,计算机无法直接对十进制的数字进行运算,这是硬件物理特性已经决定的。这样运算就分成了两个部分:先按照IEEE 754转成相应的二进制,然后对阶运算
按照这个思路分析一下0.1 + 0.2的运算过程
1.进制转换
0.1和0.2转换成二进制后会无限循环
0.1 -> 0.0001100110011001...(无限循环)
0.2 -> 0.0011001100110011...(无限循环)
但是由于IEEE 754尾数位数限制,需要将后面多余的位截掉。
下面两张图展示了浮点数在内存中的二进制表示
0.1
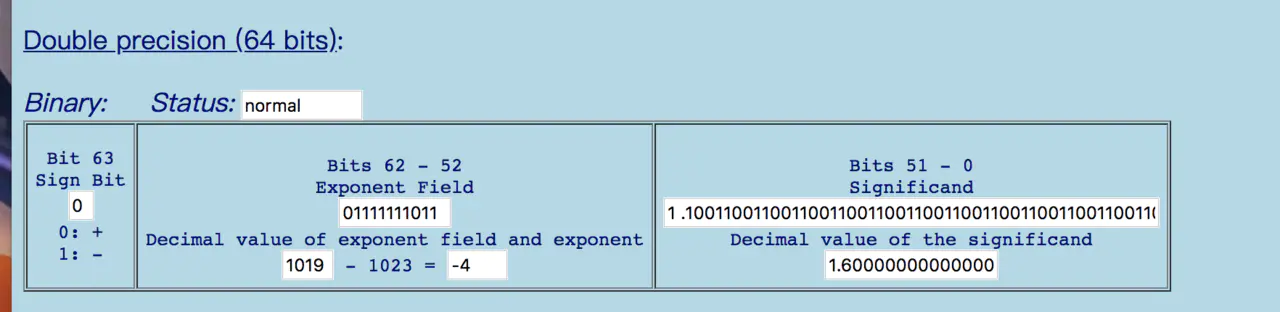
0.2

这样在进制之间的转换中精度已经损失
这里还有一个小知识点:
那为什么 x=0.1 能得到 0.1?
原因在于:标准中规定尾数f的固定长度是52位,再加上省略的一位,这53位是JS精度范围。它最大可以表示2^53(9007199254740992), 长度是 16,所以可以使用 toPrecision(16) 来做精度运算,超过的精度会自动做凑整处理。
0.10000000000000000555.toPrecision(16)
// 返回 0.1000000000000000,去掉末尾的零后正好为 0.1
// 但来一个更高的精度:
0.1.toPrecision(21) = 0.100000000000000005551
其实就是0.1也进行了进制转换,只不过因为精度超出被做了自动凑整处理,结果还是0.1.
2.对阶运算
由于指数位数不相同,运算时需要对阶运算 这部分也可能产生精度损失
按照上面两步运算(包括两步的精度损失),最后的结果是
0.0100110011001100110011001100110011001100110011001100
结果转换成十进制之后就是0.30000000000000004,这样就有了前面的“秀”操作:0.1 + 0.2 != 0.3。
所以:
精度损失可能出现在进制转化和对阶运算过程中
精度损失可能出现在进制转化和对阶运算过程中
精度损失可能出现在进制转化和对阶运算过程中
重要的事情说三遍!!!
只要在这两步中产生了精度损失,计算结果就会出现偏差。
怎么解决精度问题?
1.将数字转成整数
这是最容易想到的方法,也相对简单
function add(num1, num2) {
const num1Digits = (num1.toString().split('.')[1] || '').length;
const num2Digits = (num2.toString().split('.')[1] || '').length;
const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));
return (num1 * baseNum + num2 * baseNum) / baseNum;
}
模拟0.1+0.2情况:
(0.1*10+0.2*10)/10 = 0.3
但是这种方法对大数支持的依然不好
2.三方库
这个是比较全面的做法,推荐2个我平时接触到的库
1).Math.js
专门为 JavaScript 和 Node.js 提供的一个广泛的数学库。支持数字,大数字(超出安全数的数字),复数,分数,单位和矩阵。 功能强大,易于使用。
官网:http://mathjs.org/
GitHub:https://github.com/josdejong/mathjs
2).big.js
官网:http://mikemcl.github.io/big.js
GitHub:https://github.com/MikeMcl/big.js/
3)若干,不一一列举了
这几个类库都很牛逼,可以应对各种各样的需求,不过很多时候,一个函数能解决的问题不需要引用一个类库来解决。