
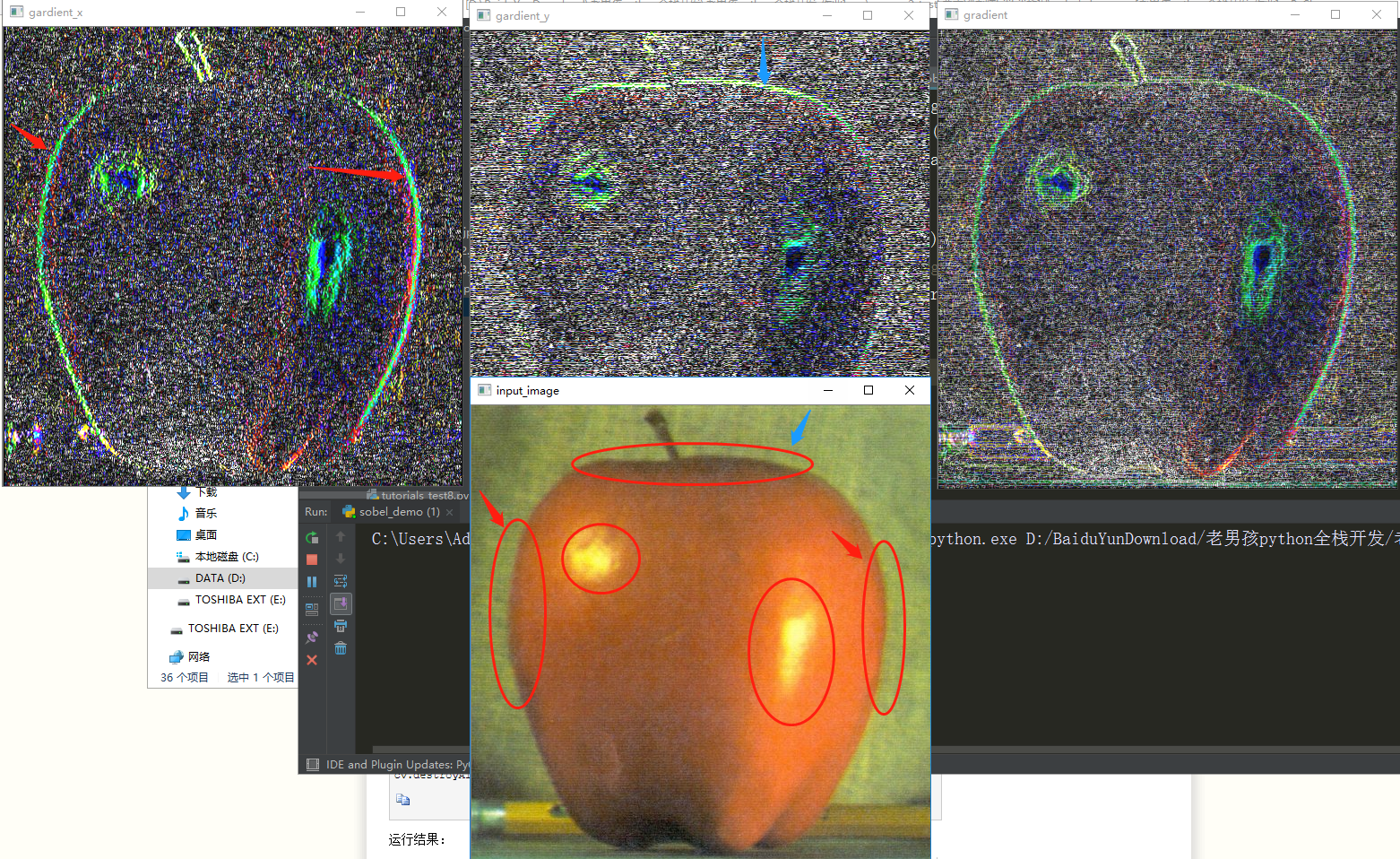
效果图:

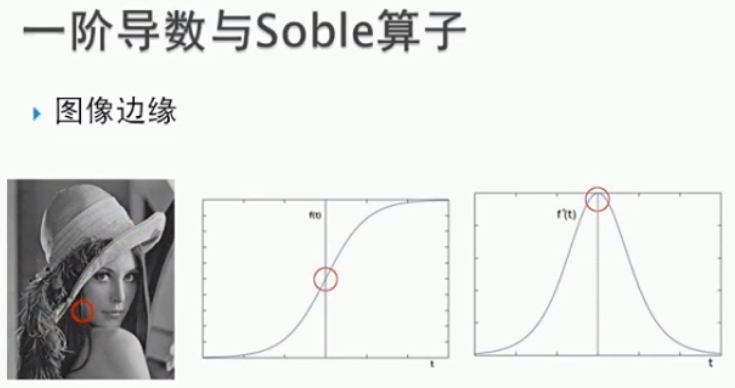
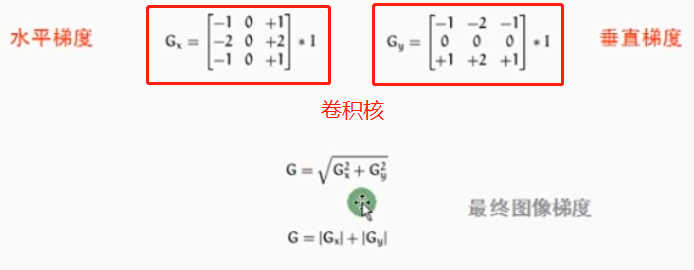
*一阶导数与Soble算子
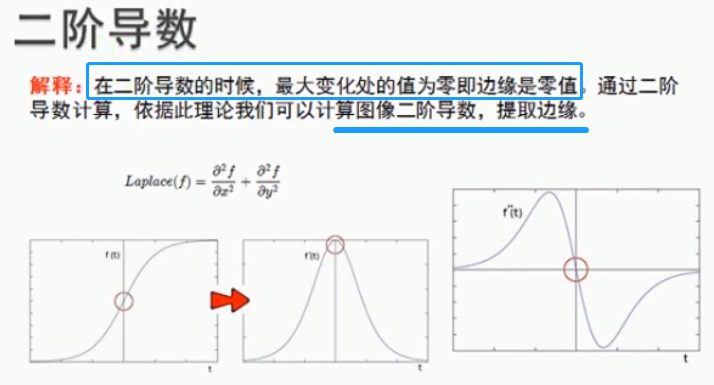
*二阶导数与拉普拉斯算子

定义:把图片想象成连续函数,因为边缘部分的像素值是与旁边像素明显有区别的,所以对图片局部求极值,就可以得到整幅图片的边缘信息了。
不过图片是二维的离散函数,图像梯度其实就是这个二维离散函数的求导。
Sobel算子是普通一阶差分,是基于寻找梯度强度。
拉普拉斯算子(二阶差分)是基于过零点检测。通过计算梯度,设置阀值,得到边缘图像。
Sobel算子效果图:
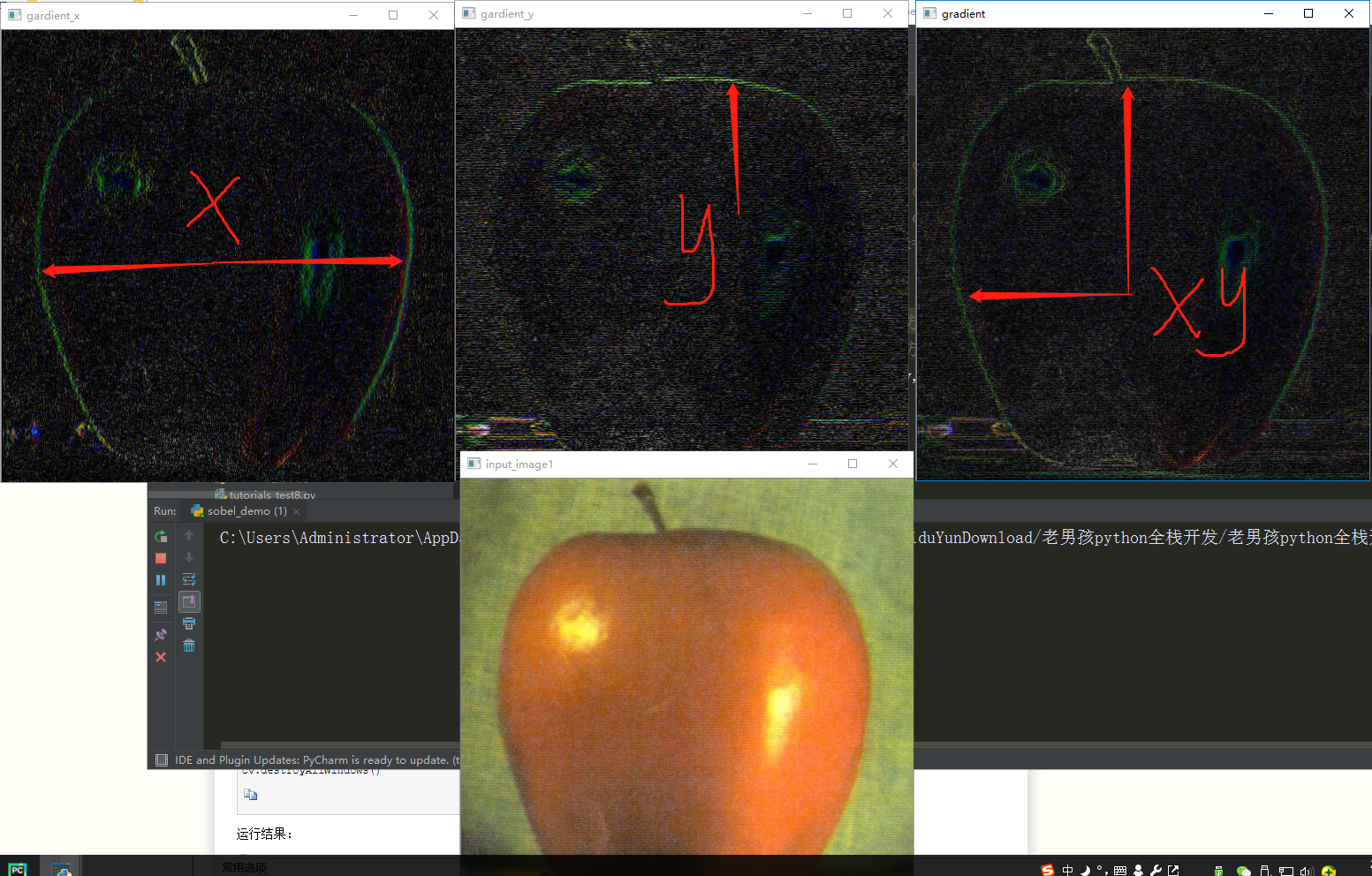
Scharr算子是Sobel的升级增强
1 import cv2 as cv 2 import numpy as np 3 4 5 #sobel算子 6 def soble_demo(image): 7 cv.imshow('input_image', src) 8 grad_x = cv.Sobel(image,cv.CV_32F,dx=1,dy=0) #对x求一阶导 9 grad_y = cv.Sobel(image,cv.CV_32F,dx=0,dy=1) #对y求一阶导 10 # grad_x = cv.Scharr(image, cv.CV_32F, dx=1, dy=0) # 对x求一阶导,Scharr算子是Sobel的升级增强 11 # grad_y = cv.Scharr(image,cv.CV_32F,dx=0,dy=1) #对y求一阶导,Scharr算子是Sobel的升级增强 12 gradx = cv.convertScaleAbs(grad_x) 13 grady = cv.convertScaleAbs(grad_y) 14 cv.imshow("gardient_x",gradx) #x方向上的梯度 15 cv.imshow("gardient_y",grady) #y方向上的梯度 16 gradxy = cv.addWeighted(gradx,0.5,grady,0.5,0) #添加xy方向上权重各为0.5,z方向权重为0,图片融合 17 cv.imshow('gradient',gradxy) 18 19 20 src = cv.imread('lena.jpg') 21 # cv.namedWindow('input_image',cv.WINDOW_AUTOSIZE) 22 cv.imshow('input_image1', src) 23 24 soble_demo(src) 25 laplace_demo(src) 26 27 cv.waitKey(0) 28 cv.destroyAllWindows()
注意:
1.Sobel算子用来计算图像灰度函数的近似梯度。Sobel算子根据像素点上下、左右邻点灰度加权差,在边缘处达到极值这一现象检测边缘。对噪声具有平滑作用,提供较为精确的边缘方向信息,边缘定位精度不够高。当对精度要求不是很高时,是一种较为常用的边缘检测方法。
2.Sobel具有平滑和微分的功效。即:Sobel算子先将图像横向或纵向平滑,然后再纵向或横向差分,得到的结果是平滑后的差分结果。
OpenCV的Sobel函数原型为:Sobel(src, ddepth, dx, dy[, dst[, ksize[, scale[, delta[, borderType]]]]]) -> dst
src参数表示输入需要处理的图像。(必需)
ddepth参数表示输出图像深度,针对不同的输入图像,输出目标图像有不同的深度。(必需)
具体组合如下:
src.depth() = CV_8U, 取ddepth =-1/CV_16S/CV_32F/CV_64F (一般源图像都为CV_8U,为了避免溢出,一般ddepth参数选择CV_32F)
src.depth() = CV_16U/CV_16S, 取ddepth =-1/CV_32F/CV_64F
src.depth() = CV_32F, 取ddepth =-1/CV_32F/CV_64F
src.depth() = CV_64F, 取ddepth = -1/CV_64F
注:ddepth =-1时,代表输出图像与输入图像相同的深度。
dx参数表示x方向上的差分阶数,1或0 。(必需)
dy参数表示y 方向上的差分阶数,1或0 。(必需)
dst参数表示输出与src相同大小和相同通道数的图像。
ksize参数表示Sobel算子的大小,必须为1、3、5、7。
scale参数表示缩放导数的比例常数,默认情况下没有伸缩系数。
delta参数表示一个可选的增量,将会加到最终的dst中,同样,默认情况下没有额外的值加到dst中。
borderType表示判断图像边界的模式。这个参数默认值为cv2.BORDER_DEFAULT。
参考:
https://blog.csdn.net/streamchuanxi/article/details/51542141
https://blog.csdn.net/sunny2038/article/details/9170013
Sobel算子原理:https://www.cnblogs.com/lancidie/archive/2011/07/17/2108885.html
注意:
Scharr算子也是计算x或y方向上的图像差分。OpenCV的Scharr函数原型为:Scharr(src, ddepth, dx, dy[, dst[, scale[, delta[, borderType]]]]) -> dst
参数和Sobel算子的几乎差不多,意思也一样,只是没有ksize大小。
2.OpenCV的convertScaleAbs函数使用线性变换转换输入数组元素成8位无符号整型。
函数原型:convertScaleAbs(src[, dst[, alpha[, beta]]]) -> dst
3.OpenCV的addWeighted函数是计算两个数组的加权和。
函数原型:addWeighted(src1, alpha, src2, beta, gamma[, dst[, dtype]]) -> dst
src1参数表示需要加权的第一个输入数组。
alpha参数表示第一个数组的权重。
src2参数表示第二个输入数组,它和第一个数组拥有相同的尺寸和通道数。
beta参数表示第二个数组的权重。
gamma参数表示一个加到权重总和上的标量值。
dst参数表示输出的数组,它和输入的两个数组拥有相同的尺寸和通道数。
dtype参数表示输出数组的可选深度。当两个输入数组具有相同的深度时,这个参数设置为-1(默认值),即等同于src1.depth()。
#laplace算子 def laplace_demo(image): dst = cv.Laplacian(image,cv.CV_32F) lpls = cv.convertScaleAbs(dst) #自定义 cv.Laplacian(),内核kernel kernel1 = np.array([[0,1,0],[1,-4,1],[0,1,0]]) #kernel1 内核相当于cv.Laplacian(src, ddepth, dst=None, ksize=1) kernel2 = np.array([[1,1,1],[1,-8,1],[1,1,1]]) #kernel2 内核相当于 dst = cv.filter2D(image,cv.CV_32F,kernel=kernel2) lpls = cv.convertScaleAbs(dst) cv.imshow("laplace_demo",lpls)
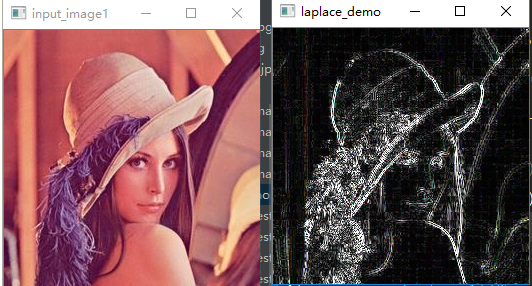
运行结果:
注意:
1.拉普拉斯算子(Laplace Operator)是n维欧几里德空间中的一个二阶微分算子,定义为梯度(▽f)的散度(▽·f)。
2.OpenCV的Laplacian函数原型为:Laplacian(src, ddepth[, dst[, ksize[, scale[, delta[, borderType]]]]]) -> dst
src参数表示输入需要处理的图像。(必需)
ddepth参数表示输出图像深度,针对不同的输入图像,输出目标图像有不同的深度。(必需)
具体组合如下:
src.depth() = CV_8U, 取ddepth =-1/CV_16S/CV_32F/CV_64F (一般源图像都为CV_8U,为了避免溢出,一般ddepth参数选择CV_32F)
src.depth() = CV_16U/CV_16S, 取ddepth =-1/CV_32F/CV_64F
src.depth() = CV_32F, 取ddepth =-1/CV_32F/CV_64F
src.depth() = CV_64F, 取ddepth = -1/CV_64F
注:ddepth =-1时,代表输出图像与输入图像相同的深度。
dst参数表示输出与src相同大小和相同通道数的图像。
ksize参数表示用于计算二阶导数滤波器的孔径大小,大小必须是正数和奇数。
scale参数表示计算拉普拉斯算子值的比例因子,默认情况下没有伸缩系数。
delta参数表示一个可选的增量,将会加到最终的dst中,同样,默认情况下没有额外的值加到dst中。
borderType表示判断图像边界的模式。这个参数默认值为cv2.BORDER_DEFAULT。
补:
这里ksize参数默认值为1,此时Laplacian()函数采用以下3x3的孔径:
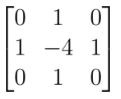
参考:
https://www.jianshu.com/p/c946cbdb6081
https://docs.opencv.org/3.0-beta/doc/py_tutorials/py_imgproc/py_gradients/py_gradients.html#gradients