题解 P4277 【河城荷取的烟花】

学校的一场考试：

点进去你也无法登陆的传送门

技能比拼，分组方案，勇士的篝火

1.国王要嫁女儿啦！OI村庄里的勇士们都想去试试，但是(不好的事都叫但是)......

2.经过OI村子里的内部选拔，很多勇士都获得了村长的青睐，村长为了......

3.OI村庄的勇士如愿娶了国王女儿，村长打算......

讲了由村长暗箱操作使一群OIER勇士娶一位公主的故事

由情节就能看出数据水的一批

【河城荷取的烟花】的情节就美了很多

T3中出现了一个美观扭曲的图片：

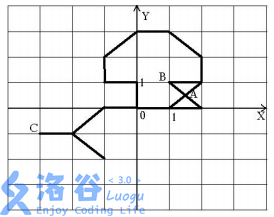
题意：

现需燃尽一摊奇怪的绳子（学校里是木棍，差不多），要找一个整点点火，使得燃尽时间最短

要明白火的（此题中）特性：

• 点燃后，火会沿着木棍向前方燃烧，可以点燃与它相接的木棍
• 只能在木棍的两端点燃。

下面是一些没多大用处的话：

---

知识点：构图+最短路应用

在此题中是一个连通图，如果我们直接构图处理比较复杂根本不会。

我们对原问题进行转换:

由于绳&棍与绳&棍之间只能在绳&棍的两端或中间相交。我们把每根绳&棍拆分成两根相等的小绳&棍，这样，绳&棍的数量增加了一倍。

原问题就转化为，绳&棍与绳&棍之间只能在绳&棍的两端相交，这样处理起来就比较方便。

我们以绳&棍为边，绳&棍与绳&棍之间的交点为顶点，构建一个连通图，问题变为寻找一个合适的顶点，使得点燃以后完全燃烧的时间最短。

---

有用的：

• 一个绳&棍可拆成两截小的绳&棍

• 很显然（“显然”是没有原因的），燃烧时间等于点燃的顶点到图中最远点的时间，如下图:

---

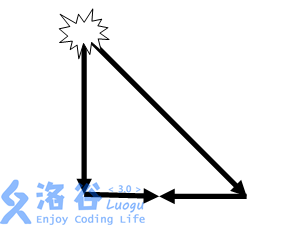
由上述，需求最短路：

于是我们怎么会有我可以利用Floyd's算法求出任意两点间的最短距离

余下还需检查每一条&根 绳&棍是否燃尽

当然，如果没有完全燃烧，应求出剩余边燃烧所需最长时间

一些有（有？）用的话：

---

对于燃烧时间为L的木棍，它的两端被点燃的时刻为T1和T2

如果T1 = T2+L 或者是 T2 = T1+L,那么燃烧到T1 和 T2 的最大时刻，这根木棍己经完全燃烧

如果T1与T2之间的时间差不等于L，那么就说明火是从不同的路径燃烧到这根木棍的两端。火将从两端向中间燃烧，并在木棍内的某个点燃完

在简单情况中，如果是从两端同时点燃，燃烧时间为L/2。

更一般地，如果T1与T2不等，我们设一端是从0时刻点燃，另一端是从T时刻点燃，那么这根木棍的燃烧时间为

T + (L-（T-0）)/2.

即，一端先燃烧T时间后，另一端才开始燃烧，完全燃烧后的时间为

（L-(T-0)）/2.

---

Floyd's :

---

#include<bits/stdc++.h>

using namespace std;

double max(double a,double b)
{
	if(a>b)return a;
	else return b;
}
double min(double a,double b)
{
	if(a<b)return a;
	else return b;
}
int n;
int a1,a2,b1,b2,a1_5,b1_5,a[10001][10001];
double t;
double e[3001][3001],dis[3001][3001];
int tot=0;
bool mid[3001];
double minx=0x7fffffff,maxx=-0x7fffffff;
int main()
{
	memset(dis,0x7fffffff,sizeof(dis));
	memset(e,0x7fffffff,sizeof(e));
	memset(mid,false,sizeof(mid));
	scanf("%d",&n);
	for(register int i=1;i<=n;i++)
	{
		scanf("%d%d%d%d%lf",&a1,&b1,&a2,&b2,&t);
		a1=a1*2+400,b1=b1*2+400,a2=a2*2+400,b2=b2*2+400;
		a1_5=(a1+a2)/2;
		b1_5=(b1+b2)/2;
		if(!a[a1][b1])a[a1][b1]=++tot;
		if(!a[a2][b2])a[a2][b2]=++tot;
		if(!a[a1_5][b1_5])
		{
			a[a1_5][b1_5]=++tot;
			mid[tot]=true;
		}
		e[a[a1][b1]][a[a1_5][b1_5]]=t*1.00000/2;
		e[a[a1_5][b1_5]][a[a1][b1]]=t*1.00000/2;
		e[a[a2][b2]][a[a1_5][b1_5]]=t*1.00000/2;
		e[a[a1_5][b1_5]][a[a2][b2]]=t*1.00000/2;
		dis[a[a1][b1]][a[a1_5][b1_5]]=t*1.00000/2;
		dis[a[a1_5][b1_5]][a[a1][b1]]=t*1.00000/2;
		dis[a[a2][b2]][a[a1_5][b1_5]]=t*1.00000/2;
		dis[a[a1_5][b1_5]][a[a2][b2]]=t*1.00000/2;
	}
	for(register int k=1;k<=tot;k++)
	{
		for(register int i=1;i<=tot;i++)
		{
			for(register int j=1;j<=tot;j++)
			{
				if(dis[i][k]<0x7fffffff&&dis[k][j]<0x7fffffff)
				{
					dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
				}
			}
		}
	}
	for(register int k=1;k<=tot;k++)
	{
		if(mid[k])continue;
		maxx=-0x7ffffff;
		for(register int i=1;i<=tot;i++)maxx=max(maxx,dis[k][i]);
		for(register int i=1;i<=tot;i++)
		{
			for(register int j=1;j<=tot;j++)
			{
				if(dis[k][i]<e[i][j]+dis[k][j]&&dis[k][j]<dis[k][i]+dis[i][j])
				{
					maxx=max(maxx,max(dis[k][i],dis[k][j])+(e[i][j]-max(dis[k][i],dis[k][j])+min(dis[k][i],dis[k][j]))/2.0);
				}
				
			}
		}
		minx=min(minx,maxx);
	}
	printf("%.4lf",minx);
	return 0;
}

---

其实，只要不直接抄题解，Ctrl+c & Ctrl+v 挺好的

但是（前面说过“但是”不是一个很好的词）上面这段代码交上洛谷不可能对

上代码是针对我校OJ的题，数据水的一批,截取:

---

【数据范围】

100%的数据：

1<=n<=40;

|a|,|b|,|c|,|d|≤200, 0≤t≤1e7;

---

运用邻接矩阵等知识点，10分不错了

做最短路方法太多了，例如SPFA，中国算法当然要用（模板好套）

有了前面代码的基础当然好写

奉上：

---

#include<bits/stdc++.h>

using namespace std;

double max(double a,double b)
{
	if(a>b)return a;
	else return b;
}
double min(double a,double b)
{
	if(a<b)return a;
	else return b;
}
struct node
{
	int from,to;
	double val;
	int nxt;
	node(int from=0,int to=0,double val=0,int nxt=0):from(from),to(to),val(val),nxt(nxt){};
};
int n,tot=0,len=0;
double val;
int a1,a2,b1,b2,am,bm;
int f[10000];
node edge[20000];
int head[10000],a[4000][4000];
double dis[10000];
bool vis[10000];
double ans=0x7fffffff;
void add(int from,int to,double val)
{
    edge[++len]=node(from,to,val,head[from]);
	head[from]=len;
}
int Num(int x,int y)
{ 
    if(!a[x][y])a[x][y]=++tot; 
	return a[x][y]; 
}
void SPFA(int s)
{
    deque<int> q;
	memset(vis,0,sizeof(vis));
	memset(dis,127,sizeof(dis));
	dis[s]=0;
	q.push_front(s);
	vis[s]=1;
	while(!q.empty())
	{
	    int cur=q.front();
		q.pop_front();
		vis[cur]=0;
		for(register int i=head[cur];i;i=edge[i].nxt)
		{
		    int id=edge[i].to;
			if(dis[id]>dis[cur]+edge[i].val)
			{
			    dis[id]=dis[cur]+edge[i].val;
				if(!vis[id])
				{
				    vis[id]=true;
					if(q.empty())q.push_front(id);
					else
					{
					    if(dis[id]<dis[q.front()])q.push_front(id);
						else q.push_back(id);
					}
				}
			}
		}
	}
}
double calculate(int x)
{
    double s=max(dis[edge[x].from],dis[edge[x].to]);
	s+=(edge[x].val-abs(dis[edge[x].from]-dis[edge[x].to]))/2;
	return s;
}
double check(int x)
{
    SPFA(x);
    double ans=0;
    for(register int i=1;i<=len;i+=2)ans=max(ans,calculate(i));
    return ans;
}
int main()
{
	scanf("%d",&n);
	for(register int i=1;i<=n;i++)
	{
        scanf("%d%d%d%d",&a1,&b1,&a2,&b2);
        a1=a1*2+2000,a2=a2*2+2000,b1=b1*2+2000,b2=b2*2+2000;
        am=(a1+a2)/2,bm=(b1+b2)/2;
		scanf("%lf",&val);
		val/=2;
        add(Num(a1,b1),Num(am,bm),val);
		add(Num(am,bm),Num(a1,b1),val);
		add(Num(a2,b2),Num(am,bm),val);
		add(Num(am,bm),Num(a2,b2),val);
		f[Num(a1,b1)]=1;
		f[Num(a2,b2)]=1;
	}
	for(register int i=1;i<=tot;i++)if(f[i])ans=min(check(i),ans);
	printf("%.4lf",ans);
	return 0;
}

---

这个SPFA自然是可过的

Floyd's算法已经有大佬写的很好，就不需要我的了~~

好不容易写出来了，当然要发题解~~ 只有一篇，过的概率大一些

我要是过不去，岂不尴尬，求过o(╥﹏╥)o

谢谢Thanks♪(･ω･)ﾉ

再见ヾ(￣▽￣)Bye_Bye