二路归并排序
分治法
分治法基本思想
将一个问题分解成若干个规模更小的子问题,子问题相互独立且与原问题性质相同,通过子问题的解,合并出原问题的解。
怎样的问题适合通过分治法解决?
- 该问题的规模缩小到一定规模就容易解决。
- 该问题能够分解成若干个规模更小的子问题,即该问题具有最优子结构性质。
- 分解出来的子问题的解,能够 合并出原问题的解。
- 子问题是相互独立的。
二路归并排序
基本思想
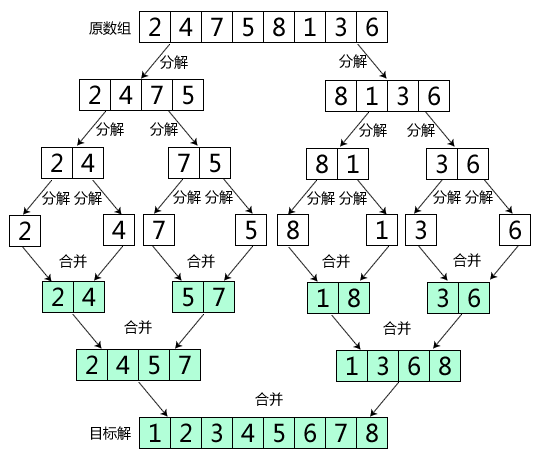
递归的对待排序序列进行对半划分,直到子序列只包含一个元素(显然,这时子序列是有序的,即子序列的排序问题已经解决)。递归的对“相邻”的子序列进行两两合并,直到合并成一个序列,即原本序列的排序问题得到解决。
基本过程
分
- 将序列对半划分,划分成两个子序列,对两个子序列进行排序后合并,原序列的排序问题即可解决。
- 重复上述过程,再次划分子序列,直到子序列中只有一个元素。
合
- 不断的对较小的有序序列进行两两合并,直到所有序列合并成一个序列。
思考
- 二路归并排序与希尔排序
同:从问题的规模入手,通过缩小问题的规模,提升问题解决效率。
异:对序列的划分方式不同,希尔排序使用某个增量,对序列进行逻辑划分,且增量会不断减小。
- 二路归并排序与快速排序
同:都借鉴了分治法思想。
异:按照上文对二路归并排序排序过程的划分方式,快速排序只有“分”的过程,在“分”的过程中完成序列的排序工作,而二路归并排序具有“分”与“合”两个过程,且真正的排序在“合”的过程中完成。