题目描述
设d(x)为x的约数个数,给定N、M,求 ∑i∑j d(i*j) (i<=n,j<=m)
输入输出格式
输入格式:
输入文件包含多组测试数据。第一行,一个整数T,表示测试数据的组数。接下来的T行,每行两个整数N、M。
输出格式:
T行,每行一个整数,表示你所求的答案。
输入输出样例
输入样例#1:
2 7 4 5 6
输出样例#1:
110 121
说明
1<=N, M<=50000
1<=T<=50000
题解:
已知推论:d(i*j)=∑a∑b[gcd(a,b)=1] (a|i , b|j)
原式化为
∑i∑j∑a∑b[gcd(a,b)=1] (1<=i<=n&&1<=j<=m)
=∑i∑j∑a∑b∑dμ(d) (d|a,d|b,d|i,d|j)
=∑i∑j∑dμ(d)∑a∑b1 (d|i,d|j,1<=a<=n/i,1<=b<=m/j)
=∑i∑j∑dμ(d)*[n/i][m/j]
=∑dμ(d)∑i∑j[n/id][m/jd] (1<=d<=min(n,m),i<=n/d,j<=m/d)
=∑dμ(d)*∑i[n/id]*∑j[m/jd]=∑dμ(d)*∑i[[n/d]/i]*∑j[[m/d]/j]
令f(x)=∑[x/i] (1<=i<=x)
接下来用分块的方法在O(N√N)时间求出f(1~n)
分块详见我写的http://www.cnblogs.com/Y-E-T-I/p/7255421.html
每一次询问的时候也用分块的方法求ans=∑dμ(d)*[f(n/d)]*[f(m/d)]
不过第三行似乎是多余的
这个结论要记下来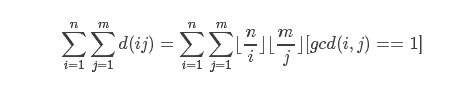
延伸结论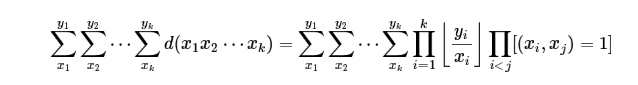
1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cstring> 5 using namespace std; 6 bool vis[50001]; 7 int tot,prime[50001],mu[50001],n,m; 8 long long ans,d[50001]; 9 void mobius() 10 {int i,j; 11 mu[1]=1; 12 for (i=2;i<=50000;i++) 13 { 14 if (vis[i]==0) 15 { 16 tot++; 17 prime[tot]=i; 18 mu[i]=-1; 19 } 20 for (j=1;j<=tot,i*prime[j]<=50000;j++) 21 { 22 vis[i*prime[j]]=1; 23 if (i%prime[j]==0) 24 { 25 mu[i*prime[j]]=0; 26 break; 27 } 28 mu[i*prime[j]]=-mu[i]; 29 } 30 } 31 for (i=1;i<=50000;i++) 32 mu[i]+=mu[i-1]; 33 } 34 void solve(int x) 35 {int i; 36 int pos=1; 37 for (i=1;i<=x;i=pos+1) 38 { 39 pos=x/(x/i); 40 d[x]+=(pos-i+1)*(x/i); 41 } 42 } 43 void work() 44 {int i; 45 ans=0; 46 int pos=1; 47 for (i=1;i<=n;i=pos+1) 48 { 49 pos=min(n/(n/i),m/(m/i)); 50 ans+=(mu[pos]-mu[i-1])*(d[n/i])*(d[m/i]); 51 } 52 } 53 int main() 54 {int i,T; 55 mobius(); 56 for (i=1;i<=50000;i++) 57 solve(i); 58 cin>>T; 59 while (T--) 60 { 61 scanf("%d%d",&n,&m); 62 if (n>m) swap(n,m); 63 work(); 64 printf("%lld ",ans); 65 } 66 }