变量名称与头文件
1 //#include <bits/stdc++.h> 2 #include <algorithm> 3 #include <iostream> 4 #include <cstdlib> 5 #include <cstring> 6 #include <sstream> 7 #include <cstdio> 8 #include <vector> 9 #include <string> 10 #include <cmath> 11 #include <queue> 12 #include <stack> 13 #include <map> 14 #include <set> 15 16 #define INF 0x3f3f3f3f 17 #define MAXN 100005 18 19 using namespace std; 20 21 struct Edge { 22 int next; 23 int to; 24 }edge[MAXN]; 25 26 int low[MAXN]; 27 int dfn[MAXN]; 28 int from[MAXN]; 29 int belong[MAXN]; 30 int instack[MAXN]; 31 int cnt_1; 32 int cnt_2; 33 int cnt_3; 34 stack<int> s1; 35 int N;
初始化
1 void init(void) { 2 memset(low, 0, sizeof(low)); 3 memset(dfn, 0, sizeof(dfn)); 4 memset(from, 0, sizeof(from)); 5 memset(belong, 0, sizeof(belong)); 6 memset(instack, 0, sizeof(instack)); 7 cnt_1 = 0; 8 cnt_2 = 0; 9 cnt_3 = 0; 10 while (s1.size()) 11 s1.pop(); 12 }
邻接表的实现
1 void add(int x, int y) { 2 edge[++cnt_1].next = from[x]; 3 edge[cnt_1].to = y; 4 from[x] = cnt_1; 5 }
核心Tarjan
1 void tarjan(int x) { 2 s1.push(x); 3 instack[x] = 1; 4 dfn[x] = low[x] = ++cnt_2; 5 for (int j = from[x]; j; j = edge[j].next) { 6 int k = edge[j].to; 7 if (!dfn[k]) { 8 tarjan(k); 9 low[x] = min(low[x], low[k]); 10 } 11 else if (instack[k] && dfn[k] < low[x]) 12 low[x] = dfn[k]; 13 } 14 if (dfn[x] == low[x]) { 15 int temp; 16 cnt_3++; 17 do { 18 temp = s1.top(); 19 s1.pop(); 20 instack[temp] = 0; 21 belong[temp] = cnt_3; 22 } while (temp != x); 23 } 24 }
接下来是对算法流程的演示。(重要,建议自己也在草稿纸上跟着模拟一下)
从节点1开始DFS,把遍历到的节点加入栈中。搜索到节点u=6时,DFN[6]=LOW[6],找到了一个强连通分量。退栈到u=v为止,{6}为一个强连通分量。
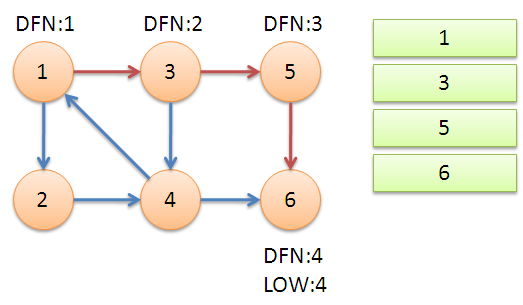
返回节点5,发现DFN[5]=LOW[5],退栈后{5}为一个强连通分量。
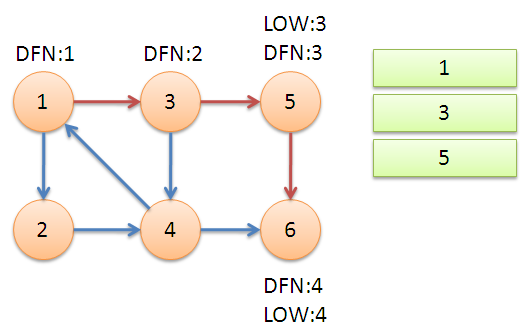
返回节点3,继续搜索到节点4,把4加入堆栈。发现节点4向节点1有后向边,节点1还在栈中,所以LOW[4]=1。节点6已经出栈,(4,6)是横叉边,返回3,(3,4)为树枝边,所以LOW[3]=LOW[4]=1。
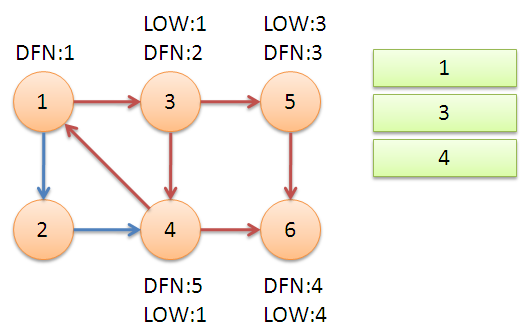
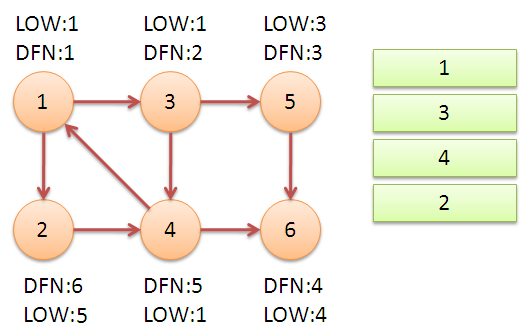
继续回到节点1,最后访问节点2。访问边(2,4),4还在栈中,所以LOW[2]=DFN[4]=5。返回1后,发现DFN[1]=LOW[1],把栈中节点全部取出,组成一个连通分量{1,3,4,2}。

至此,算法结束。经过该算法,求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。