空间几何体
- 面
- 棱
- 顶点
平面一般用 α、β、γ... 来表示
点动成线,线动成面
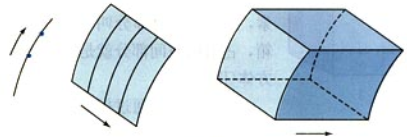
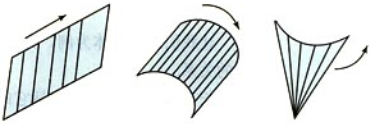
直线的平行移动,形成平面或曲面,直线绕定点转动,形成锥面
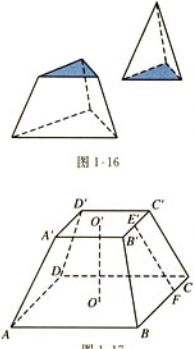
棱柱、棱锥和棱台的结构特征
多面体
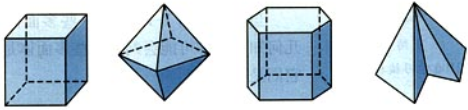
- 多面体是由若干个平面多边形围成的几何体
- 多面体的面:围成多面体的各个多边形叫做多面体的面
- 多面体的棱:相邻两个面的公共边
- 多面体的顶点:棱和棱的公共点
- 连结在同一个面上的两个顶点的线段叫做多面体对角线
- 凸多面体:一个多面体的任意一个面延展为平面,其余各面都在这个平面的同一侧
- 截面:一个几何体和一个平面相交所得到的平面图形(包含它的内部),叫做这个几何体的界面
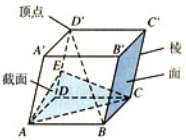
棱柱
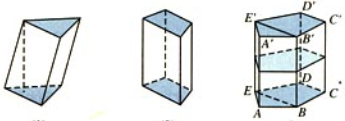
- 棱柱的两个互相平行的面叫做棱柱的底面
- 其余各面叫做棱柱的侧面,两侧面的公共边叫做棱柱的侧棱
- 如果棱柱的一个底面水平放置,则铅垂线与两底面的交点之间的线段或距离,叫做棱柱的高
- 斜棱柱,侧棱与底面不垂直的棱柱
- 直棱柱,侧棱与底面垂直的棱柱
- 正棱柱,正多边形的直棱柱
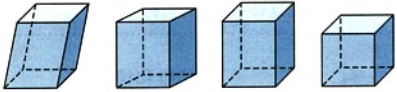
- 底面是平行四边形的棱柱叫做平行六面体
- 侧棱与底面垂直的平行六面体叫做直平行六面体
棱锥和棱台
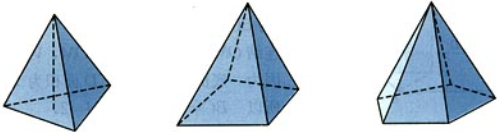
- 棱锥的侧面,棱锥中有公共顶点的各三角形,
- 棱锥的顶点,各侧面的公共顶点
- 棱锥的侧棱,相邻两侧面的公共边
- 棱锥的底面,多边形
- 棱锥的底面水平放置,顶点与过顶点,铅垂线和底面的交点之间的线段或距离,叫做棱锥的高
正棱锥
- 棱锥的底面是正多边形,并且水平放置,它的顶点又在过正多边形中心的铅垂线上,则这个棱锥叫做正棱锥
- 正棱锥各侧面都是全等的等腰三角形,这些等腰三角形底边上的高都相等,叫做棱锥的斜高
棱台
- 上底面,下底面
- 其它各面叫做棱台的侧面
- 相邻两侧面的公共边叫做棱台的侧棱
- 铅垂线和两底面交点间的线段或距离叫做棱台的高
- 正棱锥截得的棱台叫做正棱台
- 正棱台各侧面都是全等的等腰梯形,这些等腰梯形的高叫做棱台的斜高
圆柱、圆锥、圆台和球
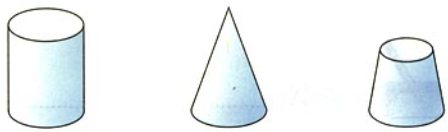
- 把圆柱看作矩形绕轴的旋转体
- 把圆锥看作三角形绕轴的旋转体
- 把圆台看作梯形绕轴的旋转体
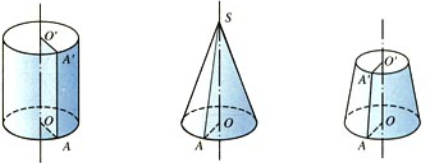
- 轴上的这条叫做几何体的高
- 垂直于轴的边旋转而成的圆面叫做这个几何体的底面
- 不垂直于轴的边旋转而成的曲面叫做这个几何体的侧面
- 无论旋转到什么位置,这条边叫做侧面的母线
球
- 球面可以看做一个半圆周绕着它的直径所在的直线旋转一周所形成的曲面,球面围成的几何体,叫做球
- 形成球的半圆的圆心叫球心
- 连结球面上一点和球心的线段叫球的半径
- 连结球面上两点且通过球心的线段叫做球的直径
- 球面也可以看作空间中到一个定点的距离等于定长的点的集合
- 球的大圆,球面被经过球心的平面截得的圆
- 球的小圆,被不经过球心的平面截得得圆
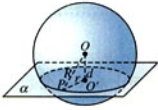
- 球面上,两点之间的最短距离,就是经过两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离
组合体
- 由柱、锥、台、球等基本几何体组合而成的