编译原理（清华大学出版社）-- 文法和语言 -- 文法的类型

0型文法

• 设G=(V_N，V_T，P，S)是一个文法，如果它的每个产生式α→β是这样一种结构：α∈(V_N ∪ V_T)^*且至少含有一个非终结符，而β∈(V_N ∪ V_T)^*，则G是一个 0型文法
• 又称短语文法，0型文法的能力相当于图灵机（Turing machine）；任何0型语言都是递归可枚举的；反之，递归可枚举集必定是一个0型语言

其他文法是对0型文法产生一些限制

1型或上下文有关的（context-sensitive）（长度增加文法）

• 设G=(V_N，V_T，P，S)是一个文法，若P中的每一个产生式 α→β均满足 |β|≥|α|（右边串的长度大于等于右边串的长度），仅仅 S→ε 除外，则文法G是 1型或上下文有关的
• 在有些定义中，将上下文有关文法的产生式的形式描述为 α₁Aα₂ → α₁βα₂ ，其中α₁、α₂ 和 β 都在（V_N ∪ V_T）^*   β≠ε，A在V_N
• 更能体现 "上下文有关"，因为只有A出现在 α₁ 和 α₂ 的上下文中，才允许用β取代A

2型或上下文无关的（context-free）（产生式的左部一定是一个非终结符）（用来判断句子正确性）

• 设G=(V_N，V_T，P，S)是一个文法，若P中的每一个产生式 α→β均满足 α是一个终结符，β∈（V_N ∪ V_T）^*，则文法G是 2型或上下文无关的
• 有时将2型文法的产生式表示为 A→β的形式，其中A∈V_N，即用β取代非终结符A时，与A所在的上下文无关，所以取名为上下文无关

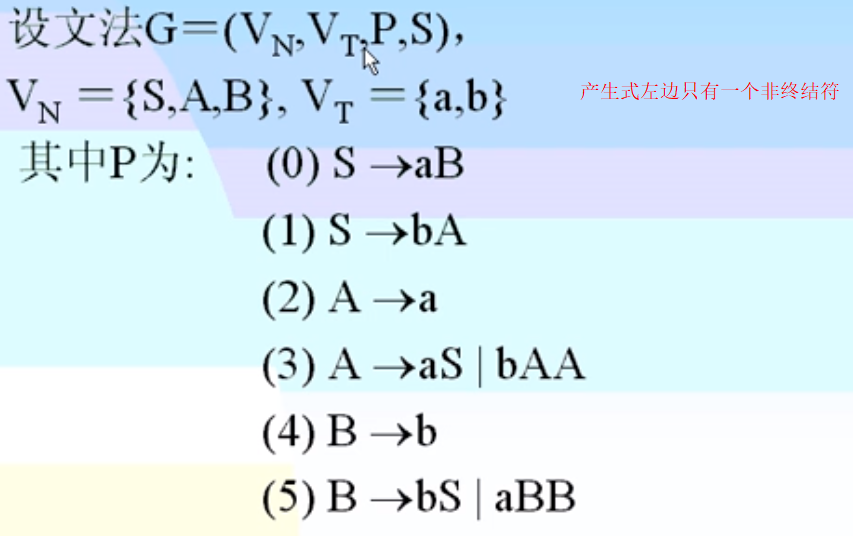
例题2.4 G=（{S，A，B}，{a，b}，P，S），其中P由下列产生式组成：

• S→aB
• A→aAA
• S→bA
• B→b
• A→a
• B→bS
• A→aS
• B→aBB

可以把相同左部的产生式，缩写为  A→α₁ | α₂ | ... | α_n  ， 这个元符号 | 读做 "或"

例题2.4的 P可以写为 

• S→aB | bA
• A → a | aS | bAA
• B → b | bS | aBB

3型文法 或 正规文法（产生式的左部一定是一个非终结符，产生式右边先终结符再非终结符或者都是终结符）（用来判断单词正确性）

• 设G=（V_N，V_T，P，S），若P中的每一个产生式的形式都是 A→aB 或 A→a，其中 A 和 B 都是非终结符，a∈V^*_T，则G是3型文法或正规文法

 

例2.5 文法G=（{S，A，B}，{0，1}，P，S），其中P由下列产生式组成：

• S→0A
• S→1B
• S→0
• S→0
• A→0A
• A→1B
• B→1B
• B→1
• B→0

G是正规文法