编译原理（清华大学出版社）-- 文法和语言 -- 上下文无关文法及其语法树

例2.6 文法G=（{E}，{+，*，i，（，）}，P，E），其中P为：

• E→i
• E→E + E
• E→E * E
• E→（E）

这里非终结符E表示一类算术表达式，i 表示程序设计语言中的变量，该文法定义了（描述了）由变量、+、*、（和）组成的算术表达式的语法结构

即： 变量是算术表达式，若E₁和E₂是算术表达式，则 E₁ + E_2、E₁ * E₂ 和（E₁）也是算术表达式

• 描述一种简单赋值语句的产生式为：（赋值语句）→i := E
• 描述条件语句的文法片段为
• <条件语句>→if<条件>then<语句>|
•                       if<条件>then<语句>else<语句>

语法树（推导树）

给定文法G=（V_N，V_T，P，S），对于G的任何句型都能构造与之关联的语法树（推导树），这棵树满足以下4个条件

• 每个结点都有一个标记，此标记是V的一个符号
• 根的标记是S
• 若一个结点n至少有一个它自己除外的子孙，并且有标记A，则A肯定在V_N中
• 如果结点n的直接子孙从左到右的次序是结点n₁,n₂,...,n_k，其标记分别为A₁，A₂，...，A_k，那么A→A₁A₂...A_k 一定是P中的一个产生式

例2.7 G=({S, A}, {a, b}, P, S)，其中P为

1. S→aAS
2. A→SbA
3. A→SS
4. S→a
5. A→ba

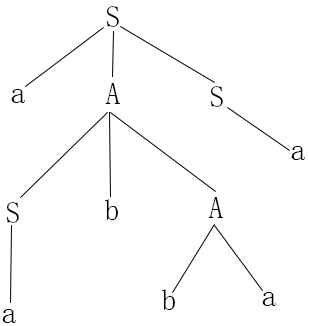
• 上图是G的一棵推导树，标记S的顶点结点是树根，它的直接子孙为a、A和S三个结点，a在A和S的左边，A在S的左边，S→aAS是一个产生式
• 同样A结点至少有一个除它自己以外的子孙（A的直接子孙为S，b和A），A肯定是非终结符
• 该图的推导树是例2.7的文法G的句型 aabbaa 的推导过程，从左到右读出推导树的叶子标记，aabbaa
• 推导过程可以多种的，
• S=>aAS=>aAa=>aSbAa=>aSbbaa=>aabbaa           （最右推导）
• S=>aAS=>aSbAS=>aabAS=>aabbaS=>aabbaa      （最左推导）
• S=>aAS=>aSbAS=>aSbAa=>aabAa=>aabbaa

如果在推导的任何一步 α=>β，其中α、β是句型都是对α中的最左（最右）非终结符进行替换，称这种推导为最左（最右推导）

最右推导，被称为规范推导，由规范推导所得的句型称为右句型或规范句型

但一个句型不一定只对应唯一的一棵语法树，例2.6的文法G就有两个不同的最左推导

   

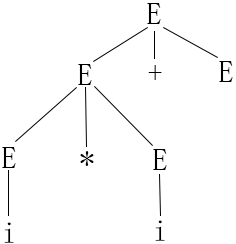
推导1：E => E+E => E*E + E => i*E + E => i*i + E => i*i + i 推导2：E => E*E => i*E => i*E + E => i*i + E => i*i + i

如果一个文法存在某个句子对应两棵不同的语法树，则说这个文法是二义的