真是亲切的1754啊。。第一道傻逼版的线段树做的是这个,后来学了zkw做的是这个,在后来决定打lrj线段树又打了一遍,如今再用splay和老朋友见面
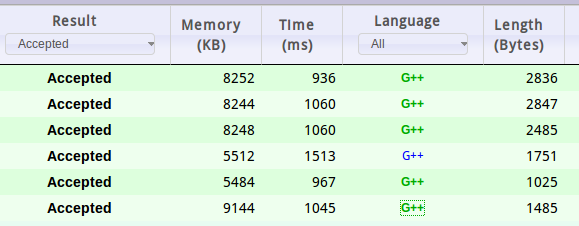 从上到下依次为:加了读入优化的splay,splay,加了inline的splay,边读入边建树的lrj线段树,zkw线段树,以及线段树初体验
从上到下依次为:加了读入优化的splay,splay,加了inline的splay,边读入边建树的lrj线段树,zkw线段树,以及线段树初体验
题意
单点修改询问区间最值。
SOL:
平衡树真是优美的植物,像陀螺通过不断的优雅的旋转体现自身的平衡与美感。
对于splay的区间问题,我们利用序号来建树,当要查询一个区间时,我们把这个区间左端点的前一个点旋到根,那么这个区间就都在根的右子树中,再将右端点的后一个点旋到根的右儿子,那么整段区间就都在根的右儿子的左儿子上了。整个过程利用BST的性质非常显然。当然为了防止越界我们把整段序列向右平移一格,便于维护。
对于这样的询问,splay与线段树没有什么区别,线段树是分割线段,而splay是取出线段,然后标记、最值、和什么的都一样了,所以线段树能实现的splay都能实现(除了可持久化。
当然对比上图,我们还是能看出它们之间的优劣。。zkw线段树继承了树状数组的优点,代码短效率高——但是貌似细节巨多。。我现在也忘得差不多了。。lrj线段树由于是nlgn的建树所以看起来稍微慢一点,实际上的效率应该在正常水平左右,打了一些注释所以代码长度显得长一些。 而splay。。。内存我多开了很多没有用的数组显得大一点。代码长度尽管以前没有用现在这么多的头文件。。但由于操作非常多尽管已经尽力把splay写得非常紧凑但还是要长处不少。
在速度上实现得和线段树差不多,看起来也挺好。
CODE:
/*==========================================================================
# Last modified: 2016-02-19 15:23
# Filename: hdu1754.cpp
# Description:
==========================================================================*/
#define me AcrossTheSky
#include <cstdio>
#include <cmath>
#include <ctime>
#include <string>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <algorithm>
#include <set>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#define lowbit(x) (x)&(-x)
#define INF 1070000000
#define FOR(i,a,b) for((i)=(a);(i)<=(b);(i)++)
#define FORP(i,a,b) for(int i=(a);i<=(b);i++)
#define FORM(i,a,b) for(int i=(a);i>=(b);i--)
#define ls(a,b) (((a)+(b)) << 1)
#define rs(a,b) (((a)+(b)) >> 1)
#define maxn 300000
#define getlc(a) ch[(a)][0]
#define getrc(a) ch[(a)][1]
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
template<class T> inline
void read(T& num) {
bool start=false,neg=false;
char c;
num=0;
while((c=getchar())!=EOF) {
if(c=='-') start=neg=true;
else if(c>='0' && c<='9') {
start=true;
num=num*10+c-'0';
} else if(start) break;
}
if(neg) num=-num;
}
/*==================split line==================*/
int root;
int n,m;
int fa[maxn],ch[maxn][2],_max[maxn],v[maxn],s[maxn],a[maxn];
int cnt=0;
int null;
inline void updata(int node){
s[node]=1+s[getlc(node)]+s[getrc(node)];
_max[node]=max(v[node],max(_max[getlc(node)],_max[getrc(node)]));
}
inline void rotate(int x){
int p=fa[x],q=fa[p],d=ch[p][1]==x;
fa[ch[p][d]=ch[x][d^1]]=p; updata(p);
fa[ch[x][d^1]=p]=x;
fa[x]=q;
if (q){
if (ch[q][0]==p) ch[q][0]=x;
else if (ch[q][1]==p) ch[q][1]=x;
}
updata(x);
}
inline void splay(int x,int &aim){
for(int y;(y=fa[x])!=aim;rotate(x))
if (fa[y]!=aim) rotate((getlc(y)==x)==(getlc(fa[y])==y)?y:x);
if (aim==0) root=x;
updata(x);
}
inline void change(int node,int x){
splay(node,null);
v[node]=x;
updata(node);
}
inline void query(int l,int r){
splay(l-1,null);
splay(r+1,root);
printf("%d
",_max[getlc(getrc(root))]);
}
inline int build(int sz){
if (sz<=0) return 0;
int t=build(sz/2),node=++cnt;
fa[ch[node][0]=t]=node;
fa[ch[node][1]=build(sz-sz/2-1)]=node;
if (node==1 || node==n+2) v[node]=-INF;
else v[node]=a[node];
updata(node);
return node;
}
int main(){
while (scanf("%d%d",&n,&m)!=EOF){
cnt=0;
memset(_max,0,sizeof(_max));
memset(fa,0,sizeof(fa));
memset(v,0,sizeof(v));
FORP(i,1,n) read(a[i+1]);
null=0;
root=build(n+2);
FORP(i,1,m){
char s[2]; scanf("%s",s); int x,y; read(x); read(y);
if (s[0]=='Q') query(x+1,y+1);
else change(x+1,y);
}
}
}