最大匹配 人员分配[邻接矩阵]

Description

设有M个工人x1, x2, …, xm，和N项工作y1, y2, …, yn，规定每个工人至多做一项工作，而每项工作至多分配一名工人去做。由于种种原因，每个工人只能胜任其中的一项或几项工作。问应怎样分配才能使尽可能多的工人分配到他胜任的工作。这个问题称为人员分配问题。

Input

第一行两个整数m，n分别为工人数和工作数。
接下来一个整数s，为二分图的边数。
接下来s行，每行两个数ai,bi表示第ai个工人能胜任第bi份工作

Output

一个整数，表示最多能让多少个工人派到自己的胜任的工作上。

Sample Input

3 3
4
1 2
2 1
3 3
1 3
Sample Output

3
Hint

规模：
1<=m,n<=100
1<=s<=10000
.
.
.
.
.
分析
人员分配问题可以用图的语言来表述。令X={x1, x2, …, xm}，Y={y1, y2, …,yn}，构造二分图G=(X, Y, E)如下：

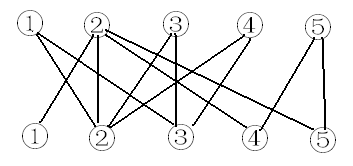
对于1≤i≤m，1≤j≤n，当且仅当工人xi胜任工作yi时，G中有一条边xiyi，

于是人员分配问题就成为在G中求一个最大匹配的问题。

为了简单起见，假设工人数等于工作数，即N=M，且N≤100，这里，N也可以看作是二分图的|X|和|Y|。
.
.
.
.
.
程序：

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
bool f[201][201],bz[300];
int a[300];
int n,m,s;

bool find(int x)
{
	for (int i=1;i<=m;i++)
		if (f[x][i]&&!bz[i])
		{
			bz[i]=true;
			int w=a[i];
			a[i]=x;
			if (w==0||find(w)) return true;
			a[i]=w;
		}
	return false;
}

int main()
{
	scanf("%d%d",&n,&m);
	scanf("%d",&s);
	memset(f,false,sizeof(f));
	for (int i=1;i<=s;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		f[x][y]=true;
	}
	for (int i=1;i<=n;i++)
	{
		memset(bz,false,sizeof(bz));
		find(i);
	}
	int ans=0;
	for (int i=1;i<=m;i++)
		if (a[i]!=0) ans++;
	printf("%d",ans);
}