Description

Input

Output
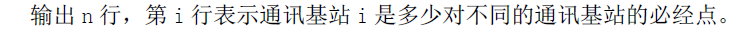
Sample Input
7 9
1 2
1 3
1 4
1 5
1 6
1 7
2 3
4 5
6 7
Sample Output
18
6
6
6
6
6
6
Data Constraint
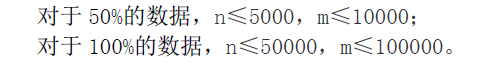
.
.
.
.
.
分析
tarjan找割点直接计算即可。对于一个点,若它是割点,那么它的贡献即为删去这个点后不同联通块的size两两相乘的和再除以二,最后加上n-1,(代表以这个点为起点的种数)。若它不是割点,那么它的贡献就是n-1。注意计算两两联通块相乘的和时,考虑x的子树中有返祖边的情况。比如这个情况:n=4,m=4,(u,v)=(1,4),(2,3),(1,2),(2,4)。对于割点的答案应是5。
.
.
.
.
.
.
程序:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
using namespace std;
int cnt=1,dfn[50100],low[50100],f[50100],ans[50100],head[200010],w[50100],n,m;
struct edge
{
int next,to;
} a[200010];
void add(int x,int y)
{
a[cnt].next=head[x];
a[cnt].to=y;
head[x]=cnt++;
}
void tarjan(int x)
{
dfn[x]=low[x]=++cnt;
w[x]=1;
int sum=0;
for (int i=head[x];i;i=a[i].next)
{
int u=a[i].to;
if (dfn[u]==0)
{
tarjan(u);
low[x]=min(low[x],low[u]);
w[x]+=w[u];
if (dfn[x]<=low[u])
{
f[x]=1;
sum+=w[u];
ans[x]+=w[u]*(n-w[u]-1);
}
} else low[x]=min(low[x],dfn[u]);
}
ans[x]+=sum*(n-sum-1);
}
int main()
{
scanf("%d%d",&n,&m);
for (int i=1;i<=m;i++)
{
int x,y;
scanf("%d%d",&x,&y);
add(x,y);
add(y,x);
}
memset(f,false,sizeof(f));
cnt=0;
tarjan(1);
for (int i=1;i<=n;i++)
printf("%d
",ans[i]/2+n-1);
return 0;
}