Description
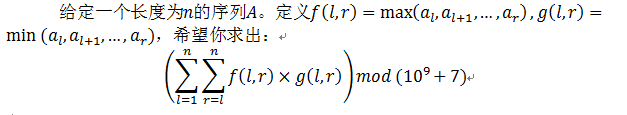
Input
输入文件名为seq.in。
首先输入n。
接下来输入n个数,描述序列 A。
Output
输出文件名为seq.out。
输出一行一个整数代表答案。
Sample Input
7
0 35 40 45 56 65 94
Sample Output
66636
Data Constraint
对于30%的数据,n<=5000
对于60%的数据,n<=50000
对于100%的数据,n<=500000,0<=A[i]<=10^9
.
.
.
.
.
分析
这题竟然用很神奇的分治?!
对于区间[x…y],将它分成三部分:
m = (x +y)/2
1.左右端点都在[x…m]里的。
2.左右端点都在[m + 1…y]里的。
3.左右端点在m的两旁。
前两个递归处理,考虑第三个怎么求,这是分治的常规套路。
先考虑区间[m + 1…y](右区间),以m+1为左端点,从左往右枚举右端点,min值会不断变小,max值会不断变大,将变化的地方存下来,分别放进两个数组里,设为a,b。
现在还要考虑区间[x…m](左区间),从m出发,从右往左枚举左端点l,记录下min值和max值,设为min_l,max_l。
最后需要将两个区间合并。
在a数组里找到代表的值第一个小于min_l的位置u(从左往右看),
在b数组里找到代表的值第一个大于max_l的位置v(从左往右看)。
这个可以二分。
由于min_l不断缩小,max_r不断变大,也可以直接维护个指针。
右端点r的取法接下来有四种情况:
1.r < min(u, v),min_[l…r] = min_l, min_[l…r] = min_r。
2.r >= max(u, v), min_[l…r] = [l…r]里的点到m+1的最小值,max_[l…r] = [l…r]里的点到m+1的最大值。
3…u <= v, u<=r < v,min_[l…r] = [l…r]里的点到m+1的最小值,max_[l…r] = min_r。
4.u >v, v<=r < u,min_[l…r] = min_l,max_[l…r] = [l…r]里的点到m+1的最大值。
1可以直接算。2、3、4维护前缀和就行了。
.
.
.
.
程序:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
long long mo=1000000007;
long long ans=0;
long long n,a[500005],u[500005],v[500005],s1[500005],s2[500005],s3[500005];
void fz(long long x,long long y)
{
if (x>y) return;
if (x==y)
{
ans=(ans+a[x]*a[x]%mo)%mo;
return;
}
long long mid=(x+y)/2;
fz(x,mid);
fz(mid+1,y);
long long uu=1,vv=1;
u[1]=v[1]=mid+1;
s1[mid]=s2[mid]=s3[mid]=0;
s1[mid+1]=s2[mid+1]=a[mid+1];
s3[mid+1]=a[mid+1]*a[mid+1];
for (int i=mid+2;i<=y;i++)
{
if (a[i]<a[u[uu]]) u[++uu]=i;
if (a[i]>a[v[vv]]) v[++vv]=i;
s1[i]=(s1[i-1]+a[u[uu]])%mo;
s2[i]=(s2[i-1]+a[v[vv]])%mo;
s3[i]=(s3[i-1]+a[u[uu]]*a[v[vv]])%mo;
}
long long minn=2147483647,maxx=-2147483647,l=1,r=1;
long long sum=ans;
for (int i=mid;i>=x;i--)
{
minn=min(minn,a[i]);
maxx=max(maxx,a[i]);
while (l<=uu&&minn<=a[u[l]]) l++;
while (r<=vv&&maxx>=a[v[r]]) r++;
long long l1,r1;
if (l>uu) l1=y; else l1=u[l]-1;
if (r>vv) r1=y; else r1=v[r]-1;
if (min(l1,r1)>mid) ans+=(long long)(min(l1, r1)-mid)*minn%mo*maxx%mo;
if (max(l1,r1)<y) ans+=s3[y]-s3[max(l1,r1)];
if (l1<=r1) ans+=(long long)(s1[r1]-s1[l1])*maxx%mo; else ans+=(long long)minn*(s2[l1]-s2[r1])%mo;
ans=(ans%mo+mo)%mo;
}
}
int main() {
freopen("seq.in","r",stdin);
freopen("seq.out","w",stdout);
scanf("%lld",&n);
for (int i=1;i<=n;i++)
scanf("%lld",&a[i]);
fz(1,n);
printf("%lld",ans);
fclose(stdin);
fclose(stdout);
return 0;
}