食物

Description

Input

Output

Sample Input
4
1 1 7
14 2 1
1 2 2
1 1 10
10 10 1
5 7 2
5 3 34
1 4 1
9 4 2
5 3 3
1 3 3
5 3 2
3 4 5
6 7 5
5 3 8
1 1 1
1 2 1
1 1 1

Sample Output
4
14
12
TAT

Data Constraint

.
.
.
.
.
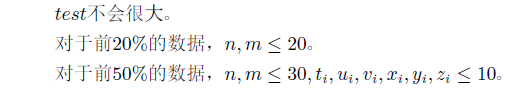
分析
题目大意：有n种食物，和m种交通工具，问在费用不超过50000和美味度大于等于p时，需要的最少的运输费

这显然是一个多重背包问题
设f[i]为食物大小为i的时候所能得到的最大美味度，转移显然，f[i]=min(f[i-u]+t)
再设g[i]为费用为i的时候所能得到的最大运输量，转移也显然，g[i]=min(g[i-y]+x)
最后的话，然后使f[g[i]]>=p的时候，ans取一个min就好了

然而这样做会超时

那么我们用二进制优化
二进制优化其实就是将其变成1、2、4、8、16…的形式
这样做，既可以将所有的状态给表示出来，也可以很有效的减少循环状态数、数组的大小

.
.
.
.
.
程序：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;

int f[50100],g[50100];

inline int read()
{
   int s=0,w=1;
   char ch=getchar();
   while (ch<'0'||ch>'9'){if(ch=='-')w=-1;ch=getchar();}
   while (ch>='0'&&ch<='9') s=s*10+ch-'0',ch=getchar();
   return s*w;
}

int main()
{
	int t1;
	t1=read();
	while (t1--)
	{
		int n,m,p;
		n=read();m=read();p=read();
		memset(f,0,sizeof(f));
		for (int i=1;i<=n;i++)
		{
			int t,u,w;
			t=read();u=read();w=read();
			for (int j=1;j<=w;j*=2)
			{
				for (int k=20000;k>=u*j;k--)
					f[k]=max(f[k],f[k-u*j]+t*j);
				w-=j;
			}
			if (w!=0) 
			{
				for (int k=20000;k>=u*w;k--)
					f[k]=max(f[k],f[k-u*w]+t*w);
			}
		}
		memset(g,0,sizeof(g));
		for (int i=1;i<=m;i++)
		{
			int x,y,z;
			x=read();y=read();z=read();
			for (int j=1;j<=z;j*=2)
			{
				for (int k=50000;k>=y*j;k--)
					g[k]=max(g[k],g[k-y*j]+x*j);
				z-=j;
			}
			if (z!=0) 
			{
				for (int k=50000;k>=y*z;k--)
					g[k]=max(g[k],g[k-y*z]+x*z);
			}
		}
		int ans=0;
		for (int i=1;i<=50000;i++)
			if (f[g[i]]>=p)
			{
				ans=i;
				break;
			}
		if (ans!=0) printf("%d
",ans); else printf("TAT
");
	}
	return 0;
}