Description
网上出现了一种高科技产品——人品测试器。只要你把你的真实姓名输入进去,系统将自动输出你的人品指数。yzx不相信自己的人品为0。经过了许多研究后,yzx得出了一个更为科学的人品计算方法。这种方法的理论依据是一个非常重要的结论:人品具有遗传性。因此,一个人的人品完全由他的祖先决定。yzx提出的人品计算方法相当简单,只需要将测试对象的k个祖先的人品指数(可能为负数)加起来即可。选择哪k个祖先可以由测试者自己决定,但必须要满足这个要求:如果除自己的父母之外的某个祖先被选了,那么他的下一代必需要选(不允许跳过某一代选择更远的祖先,否则将失去遗传的意义)。
非常不幸的是,yzx测试了若干次,他的人品值仍然不能为一个正数。现在yzx需要你帮助他找到选择祖先的最优方案,使得他的人品值最大。
Input
第一行是两个用空格隔开的正整数n和k,其中n代表yzx已知的家谱中共有多少人(包括yzx本身在内),k的意义参见问题描述。
第二行有n-1个用空格隔开的整数(可能为负),这些数的绝对值在2^15以内。其中,第i个数表示编号为i+1的人的人品值。我们规定,编号为1的人是yzx。
接下来n行每行有两个用空格隔开的数,其中第i行的两个数分别表示第i个人的父亲和母亲的编号。如果某个人的父亲或母亲不在这个家谱内,则在表示他的父亲或母亲的编号时用0代替。
除yzx以外的所有人都是yzx的祖先,他们都会作为父亲或母亲被描述到。每个人都不可能同时作为多个人的父亲或者是母亲。
Output
一个整数,表示yzx能够得到的最大人品值。
Sample Input
6 3
-2 3 -2 3 -1
2 3
4 5
0 6
0 0
0 0
0 0
Sample Output
4
样例说明下图显示了输入样例所描述的家谱图。括号里的数表示的是该人的人品值。
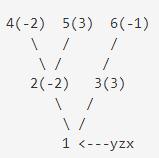
显然,选择祖先2、3、5能使yzx的人品值达到最大。这个最大值为4,表示yzx能够得到的最大人品值。
Data Constraint
50%的数据,n<=10。
100%的数据,n<=100。
.
.
.
.
.
.
分析
树形DP
.
.
.
.
.
程序:
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
bool f[200][200];
long long dp[200][200];
int l[200],r[200],rp[200];
int dfs(int num,int tj)
{
if (f[num][tj]==true) return dp[num][tj];
if (tj==0)
{
dp[num][tj]=0;
return dp[num][tj];
}
if (num==0)
{
dp[num][tj]=-2147483647;
return dp[num][tj];
}
if (tj==1)
{
dp[num][tj]=rp[num];
return dp[num][tj];
}
long long ans=-2147483647;
for (int i=0;i<=tj-1;i++)
ans=max(ans,(long long)rp[num]+dfs(l[num],i)+dfs(r[num],tj-i-1));
f[num][tj]=true;
dp[num][tj]=ans;
return ans;
}
int main()
{
int n,k;
scanf("%d%d",&n,&k);
rp[1]=0;
for (int i=2;i<=n;i++)
scanf("%d",&rp[i]);
for (int i=1;i<=n;i++)
scanf("%d%d",&l[i],&r[i]);
memset(f,false,sizeof(f));
printf("%d",dfs(1,k+1));
return 0;
}