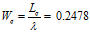在现实生活中排队的现象可说是无处不在,如:买票、超商、百货公司…等。顾客总是在揣测"排在哪一个服务台会比较快?"或"到底还要排多久呢?"类似这样的问题;相对的,由经营者的立场也在思考在什么时间点要开设几个服务窗口才能降低成本且达到最大的效益。为了探讨这类问题,数学家们逐渐发展出了名为"排队理论(Queuing theory)"的工具。排队理论主要是利用机率的假设做为分析条件,顾名思义是一套研究排队等候时间问题的工具。排队理论由丹麦的学者Erlang在1910年左右首先提出来的,起初是为了解决电话网路中顾客等候时间的问题,接着由俄国数学家Markov建立了所谓的马可夫模型(Markov Model)。而Kendall在1953年提出了A/B/C/X/Y/Z表示法,其中
|
A |
顾客进入系统中所服从的机率分配模型。 (如:来电量) |
|
B |
服务时间长短所服从的机率分配模型。 (如:通话时间) |
|
C |
服务台的个数。 (如:座席数) |
|
X |
平行队列的数目。 |
|
Y |
系统最大容量。 |
|
Z |
意指排队纪律,通常有FCFS先到先服务、LCFS后来服务与RSS随机服务等型式。 |
将排队理论复杂的假设以简单明确的方式表示。排队理论发展至今,已被广泛应用在网路通讯、生产、运输和库存等各项资源共享的随机服务系统。而Erlang C与M/M/N排队模型是具有相同的假设,如下
(1) 顾客到达服从参数为的Poisson随机过程。 (M)
(2) 服务时间服从参数为的指数机率分配。 (M)
(3) 服务台个数为N个。 (N)
(4) 平行对列数目为1。
(5) 系统最大容量无限多个顾客在系统中。
(6) FCFS先来先服务。
二参数定义与公式
|
参数 |
定义 |
公式与实例 (座席数=25位) (每15分钟来电量=100通) (平均处理时间=180秒) |
|
|
每单位时间顾客到达率 |
|
|
|
每单位时间的服务率 |
|
|
|
系统负载率, |
|
|
|
无顾客在系统中的机率 |
|
|
|
顾客必须等候的机率 |
|
|
|
期望排队长度 |
|
|
|
期望排队等候时间 |
|
|
|
服务水准(Sever Level),在t秒内接起的机率 |
|