参考博客:https://www.cnblogs.com/guoyaohua/p/8724433.html
BN好处:
1)防止梯度消失,提升训练速度,收敛过程更快。因为把输入分布拉到了例如sigmoid中间区域
2)增加分类效果,类似于dropout的一种防止过拟合的正则化表达方式,不用dropout也能达到相当的效果
3) 调参过程简单许多,对初始化要求没有那么高,而且可以使用大的学习率。
关于第1点,有个疑问,如果是用relu激活函数,就不存在类似sigmoid、tanh的梯度饱和区,为什么也还要用BN呢?
经百度查询,有网友说:
不论用不用BN,relu该有的缺点也都不会少,例如有节点dead。而用了BN后,至少保证了一部分节点一定是active的。简而言之,就是也不会更差吧。
关于2、3点我个人不是很理解,经网上查询,总结如下:
BN主要作用是加快网络的训练速度。关于防止过拟合可理解为:
理解1)BN每次mini-batch的数据不同,但每次都对这些数据进行了规范化(移动了mean和var),可以认为是引入了噪声,相当于进行了data augmentation
(https://www.zhihu.com/question/275788133/answer/384198714)
理解2)
BN的核心是通过对参数搜索空间进行约束来增加鲁棒性,这种约束压缩了搜索空间,改善了系统的结构合理性,比如加速收敛,保证梯度,缓解过拟合等。BN就是要保证曲线分布尽量均匀平滑均匀(数据的各个维度上尺度一致从而避免出现某些维度数据过于集中),这可以带来缓解梯度消失和过拟合。同样,dropout是在另一个角度对曲线分布进行约束,其要求是当仅考察数据的任意一个低维子空间的时候,曲线的分布也是均匀的。BN和dropout从不同角度对曲线分布进行约束,二者有相似的作用,但是有时候又会相互冲突,因为毕竟二者所限定的约束不能完全互容,所以二者有时候可以替代,但又不能完全替代。
(https://www.zhihu.com/question/275788133/answer/386749776)
BN一句话概括:
对于每个隐层神经元,把逐渐向两端靠拢的分布强行拉回标准正态分布,使得非线性函数的输入落在比较敏感的区域,以避免梯度消失问题。
BN基本思想:
对深层神经网络而言,随层数越深,其每层输入值的整体分布一般逐渐往非线性函数的饱和区(例如下图sigmoid的两端)。这导致反向传播时,低层神经网络的梯度消失,更新缓慢。
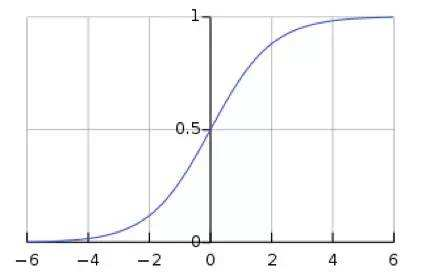
BN则是把每层神经网络任意神经元的输入值分布强行拉回均值为0,方差为1的标准正态分布。即将越来越偏的分布强行拉回比较标准的分布,使得激活输入值落在非线性函数对对输入比较敏感的中间区域。例如标准正态分布,有64%概率x落在[-1, 1]之间,95%的概率落在[-2, 2]范围内。
这样 输入的小变化会导致损失函数较大的变化,使得梯度变大,避免梯度消失问题产生(连乘);同时梯度变大意味学习收敛速度更快,也可加快训练速度。
scale and shift
经过BN后,大部分输入的值落在非线性函数的线性区内,其对应的导数原来饱和区(非线性区),但这不就使得非线性函数和线性函数效果相同了?
如果是多层的线性变换,深层是没有意义的,因为多层线性和一层线性是等价的。岂不是意味着网络的表达能力下降了?
所以BN为了保证非线性的获得,对变换后的标准正态分布又进行了scale加上shift的操作(y=x*scale+shift),每个神经元增加了两个参数scale和shift,这两个参数是通过训练学习得到的。通过这两个参数,可以将标准正态分布左移或右移并长胖或变瘦一点。每个实例挪动的程度不一。这样等价于把非线性函数的值从正中间线性区域往非线性挪动了。
核心思想就是找到一个线性和非线性较好的平衡点,即可享受非线性的较强表达能力的好处,也可避免太靠近非线性区两头使得网络收敛速度太慢。有了这两个参数,就保证了至少不会比原来更差,因为还可以变回原来的样子。
训练阶段的BN
假设一个深层神经网络,其中两层结构如下:
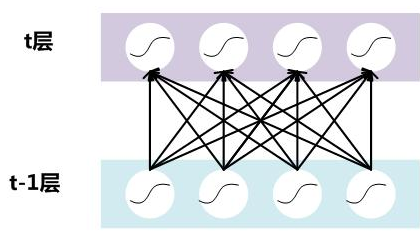
要对每个隐层神经元的激活值做BN,即对每个隐层又加上一个BN操作层。BN操作层位于上一层激活值获得并计算Y=WX+B后,下一层非线性函数变换(激活层)之前,如下:

对于mini-batch SGD来说,一次训练包含m个训练实例,BN操作就是对隐层内每个神经元的输入,进行标准正态分布归一化操作,均值和方差都有这m个训练实例求出。
论文中的描述如下:

推理阶段的BN
在训练时,BN根据mini-batch中若干训练样本进行激活数值的调整,但在推理时,输入只有一个实例,而一个实例无法求实例集合的均值和方差,如何做BN呢?
可以用从所有训练实例中获得的统计量来作为推理中的均值和方差。但如果直接算全局统计量,计算量太大。所以需将之前训练步骤时,每个mini-batch的均值和方差记录,然后对这些均值和方差求对应的数学期望,即可算出全局统计量。
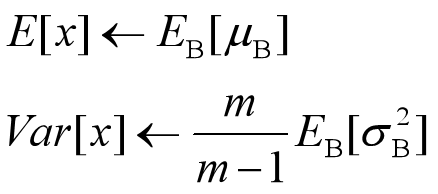
有了均值和方差后,每个隐层神经元也已经有了对应训练好的scaling和shift参数,就可以进行推理时的BN变换了:

与训练时的公式是等价的,如下:
![]()
为什么要写成上上式这个形式呢?因为实际推理运行时,对每个隐层节点来说E,var都是固定值,可以减少计算量。不然用上式,每次推理的时候都要重新计算一下。
学习记录,如有描述不对或欠妥的地方,欢迎大家指出讨论~