zoukankan      html  css  js  c++  java

  • GRU(Gated Recurrent Unit) 更新过程推导及简单代码实现

    GRU(Gated Recurrent Unit) 更新过程推导及简单代码实现

    RNN
    GRU
    matlab codes

    RNN网络考虑到了具有时间数列的样本数据，但是RNN仍存在着一些问题，比如随着时间的推移，RNN单元就失去了对很久之前信息的保存和处理的能力，而且存在着gradient vanishing问题。
    所以有些特殊类型的RNN网络相继被提出，比如LSTM(long short term memory)和GRU(gated recurrent unit)(Chao,et al. 2014).这里我主要推导一下GRU参数的迭代过程

    GRU单元结构如下图所示

    enter description here

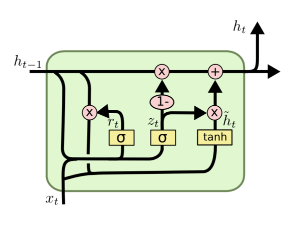
    1479126283494.jpg

    数据流过程如下

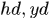    其中表示Hadamard积，即对应元素乘积；下标表示节点的index，上标表示时刻；表示隐层到输出层的参数矩阵,分别是隐层和输出层的节点个数；分别表示输入和上一时刻隐层到更新门z的连接矩阵，表示输入数据的维度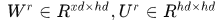；分别表示输入和上一时刻隐层到重置门r的连接矩阵；分别表示输入和上一时刻的隐层到待选状态的连接矩阵。

    针对于时刻t，使用链式求导法则，计算参数矩阵的梯度,其中E是代价函数，首先计算对隐层输出的梯度，因为隐层输出牵涉到多个时刻

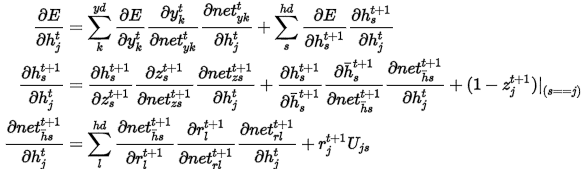
    所以

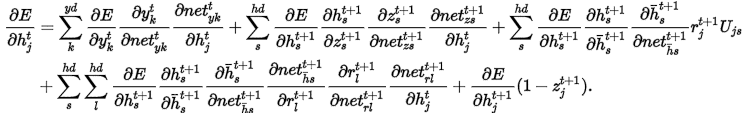
    其中分别是对应激活函数的线性和部分
    现在对参数计算梯度

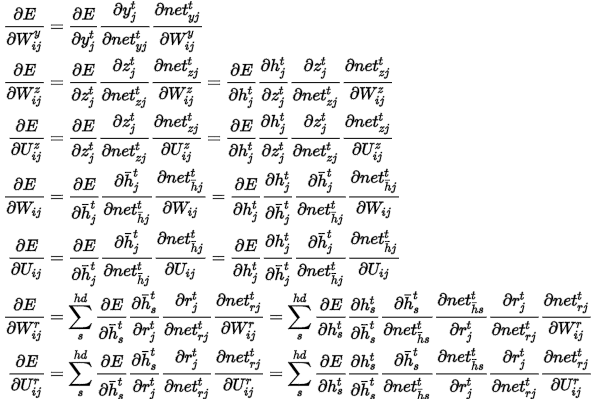
    令

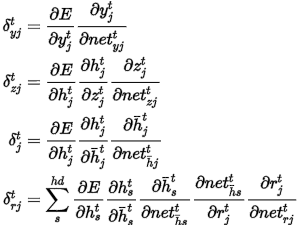
    则

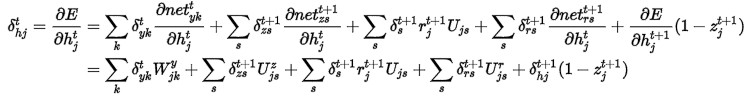
    将上面的式子矢量化(行向量)表示：

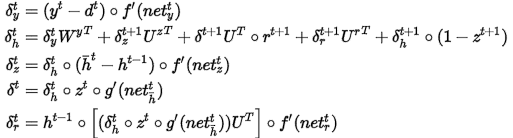
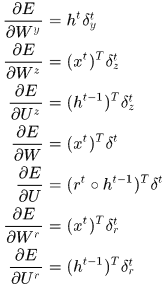
    那接下来使用matlab来实现一个小例子，看看GRU的效果，同样是二进制相加的问题

    1. function error= GRUtest( ) 
    2. % 初始化训练数据 
    3. uNum=16;%单元个数 
    4. maxInt=2^uNum; 
    5. % 初始化网络结构 
    6. xdim=2; 
    7. ydim=1; 
    8. hdim=16; 
    9. eta=0.1; 
    10. %初始化网络参数 
    11. Wy=rand(hdim,ydim)*2-1; 
    12. Wr=rand(xdim,hdim)*2-1; 
    13. Ur=rand(hdim,hdim)*2-1; 
    14. W =rand(xdim,hdim)*2-1; 
    15. U =rand(hdim,hdim)*2-1; 
    16. Wz=rand(xdim,hdim)*2-1; 
    17. Uz=rand(hdim,hdim)*2-1; 
    18.  
    19. rvalues=zeros(uNum+1,hdim); 
    20. zvalues=zeros(uNum+1,hdim); 
    21. hbarvalues=zeros(uNum,hdim); 
    22. hvalues = zeros(uNum,hdim); 
    23. yvalues=zeros(uNum,ydim); 
    24.  
    25. for p=1:10000 
    26. aInt=randi(maxInt/2); 
    27. bInt=randi(maxInt/2); 
    28. cInt=aInt+bInt; 
    29. at=dec2bin(aInt)-'0'; 
    30. bt=dec2bin(bInt)-'0'; 
    31. ct=dec2bin(cInt)-'0'; 
    32. a=zeros(1,uNum); 
    33. b=zeros(1,uNum); 
    34. c=zeros(1,uNum); 
    35. a(1:size(at,2))=at(end:-1:1); 
    36. b(1:size(bt,2))=bt(end:-1:1); 
    37. c(1:size(ct,2))=ct(end:-1:1); 
    38. xvalues=[a;b]'; 
    39. d=c'; 
    40.  
    41. % 前向计算 
    42. rvalues(1,:)=sigmoid(xvalues(1,:)*Wr); 
    43. hbarvalues(1,:)=outTanh(xvalues(1,:)*W); 
    44. zvalues(1,:)=sigmoid(xvalues(1,:)*Wz); 
    45. hvalues(1,:)=zvalues(1,:).*hbarvalues(1,:); 
    46. yvalues(1,:)=sigmoid(hvalues(1,:)*Wy); 
    47. for t=2:uNum 
    48. rvalues(t,:)=sigmoid(xvalues(t,:)*Wr+hvalues(t-1,:)*Ur); 
    49. hbarvalues(t,:)=outTanh(xvalues(t,:)*W+(rvalues(t,:).*hvalues(t-1,:))*U); 
    50. zvalues(t,:)=sigmoid(xvalues(t,:)*Wz+hvalues(t-1,:)*Uz); 
    51. hvalues(t,:)=(1-zvalues(t,:)).*hvalues(t-1,:)+zvalues(t,:).*hbarvalues(t,:); 
    52. yvalues(t,:)=sigmoid(hvalues(t,:)*Wy);  
    53. end 
    54.  
    55. % 误差反向传播 
    56. delta_r_next=zeros(1,hdim); 
    57. delta_z_next=zeros(1,hdim); 
    58. delta_h_next=zeros(1,hdim); 
    59. delta_next=zeros(1,hdim); 
    60.  
    61. dWy=zeros(hdim,ydim); 
    62. dWr=zeros(xdim,hdim); 
    63. dUr=zeros(hdim,hdim); 
    64. dW=zeros(xdim,hdim); 
    65. dU=zeros(hdim,hdim); 
    66. dWz=zeros(xdim,hdim); 
    67. dUz=zeros(hdim,hdim); 
    68.  
    69. for t=uNum:-1:2 
    70. delta_y=(yvalues(t,:)-d(t,:)).*diffsigmoid(yvalues(t,:)); 
    71. delta_h=delta_y*Wy'+delta_z_next*Uz'+delta_next*U'.*rvalues(t+1,:)+delta_r_next*Ur'+delta_h_next.*(1-zvalues(t+1,:)); 
    72. delta_z=delta_h.*(hbarvalues(t,:)-hvalues(t-1,:)).*diffsigmoid(zvalues(t,:)); 
    73. delta =delta_h.*zvalues(t,:).*diffoutTanh(hbarvalues(t,:)); 
    74. delta_r=hvalues(t-1,:).*((delta_h.*zvalues(t,:).*diffoutTanh(hbarvalues(t,:)))*U').*diffsigmoid(rvalues(t,:)); 
    75.  
    76. dWy=dWy+hvalues(t,:)'*delta_y; 
    77. dWz=dWz+xvalues(t,:)'*delta_z; 
    78. dUz=dUz+hvalues(t-1,:)'*delta_z; 
    79. dW =dW+xvalues(t,:)'*delta; 
    80. dU =dU+(rvalues(t,:).*hvalues(t-1,:))'*delta ; 
    81. dWr=dWr+xvalues(t,:)'*delta_r; 
    82. dUr=dUr+hvalues(t-1,:)'*delta_r; 
    83.  
    84. delta_r_next=delta_r; 
    85. delta_z_next=delta_z; 
    86. delta_h_next=delta_h; 
    87. delta_next =delta; 
    88.  
    89. end 
    90.  
    91. t=1; 
    92. delta_y=(yvalues(t,:)-d(t,:)).*diffsigmoid(yvalues(t,:)); 
    93. delta_h=delta_y*Wy'+delta_z_next*Uz'+delta_next*U'.*rvalues(t+1,:)+delta_r_next*Ur'+delta_h_next.*(1-zvalues(t+1,:)); 
    94. delta_z=delta_h.*(hbarvalues(t,:)-0).*diffsigmoid(zvalues(t,:)); 
    95. delta =delta_h.*zvalues(t,:).*diffoutTanh(hbarvalues(t,:)); 
    96. delta_r=0.*((delta_h.*zvalues(t,:).*diffoutTanh(hbarvalues(t,:)))*U').*diffsigmoid(rvalues(t,:)); 
    97.  
    98. dWy=dWy+hvalues(t,:)'*delta_y; 
    99. dWz=dWz+xvalues(t,:)'*delta_z; 
    100. dW =dW+xvalues(t,:)'*delta; 
    101. dWr=dWr+xvalues(t,:)'*delta_r; 
    102.  
    103. Wy = Wy-eta*dWy; 
    104. Wr = Wr-eta*dWr; 
    105. Ur = Ur-eta*dUr; 
    106. W = W -eta*dW; 
    107. U = U-eta*dU; 
    108. Wz = Wz-eta*dWz; 
    109. Uz = Uz-eta*dUz; 
    110. error = (norm(yvalues-d,2))/2.0; 
    111. %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 
    112. if mod(p,500)==0 
    113. fprintf('******************第%s次迭代**************** ',int2str(p)); 
    114. yvalues=round(yvalues(end:-1:1)); 
    115. y=bin2dec(int2str(yvalues')); 
    116. fprintf('y=%d ',y); 
    117. fprintf('c=%d ',cInt); 
    118. fprintf('样本误差:e=%f ',error); 
    119. end 
    120. end 
    121. end 
    122.  
    123. function f=sigmoid(x) 
    124. f=1./(1+exp(-x)); 
    125. end 
    126.  
    127. function fd = diffsigmoid(f) 
    128. fd=f.*(1-f); 
    129. end 
    130.  
    131. function g=outTanh(x) 
    132. g=1-2./(1+exp(2*x)); 
    133. end 
    134.  
    135. function gd=diffoutTanh(g) 
    136. gd=1-g.^2; 
    137. end 

    部分实验结果

    enter description here

    1479392393541.jpg
  • 相关阅读:
    MonkeyScript_API
    APP性能（Monkey）【启动时间、CPU、流量、电量、内存、FPS、过度渲染】
    adb基本命令 & Monkey发生随机事件命令及参数说明
    MonkeyRunner_API
    2021春招冲刺-1218 页面置换算法 | sort的原理 | 语义化标签 | 标签的继承
    2021春招冲刺-1217 线程与进程 | ES6语法 | h5新增标签
    2021春招冲刺-1216 死锁 | 箭头函数 | 内联元素 | 页面渲染
    【unity】旧世开发日志
    HTTP 与HTTPS 简单理解
    GET POST 区分
  • 原文地址：https://www.cnblogs.com/YiXiaoZhou/p/6075777.html
Copyright © 2011-2022 走看看