20172314 2018-2019-1《程序设计与数据结构》第九周学习总结

教材学习内容总结

无向图

• 图与树类似，由顶点和边连接构成。图只有顶点没有边时，也是图，是一种特殊形式。

• 边由相互连通的结点对表示，（A,B）表示从顶点A到顶点B有一条边，无序结点对表示顶点A，B之间的边可以从两个方向游历，边记做（A,,B）或（B,A）均可

• 无向图就是边全为无序结点对的图
  

• 两个顶点之间若有连通边，则称这两个顶点是邻接的。他们互为邻居

• 路径表示一系列的边，路径的长度表示路径中边的条数（或顶点数减一）；无向图中路径ABD与路径DBA等同。

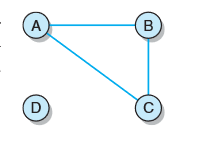
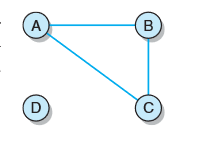
• 注意区分：如果无向图拥有最大数目的连通顶点的边，则无向图是完全的；如果无向图中任意两个顶点之间都存在一条路径，则认为无向图是连通的。如图是非连通无向图，D与另外三个顶点之间均没有任何路径。
  

• 注意区分：联通一个节点及其自身的边称为自循环或环，边（A,A）表示连接A到自身的一个环；环路是一种首顶点和末顶点相同且没有重边的路径

• 没有环路的图称为无环的

• 无向树是一种连通的无环无向图，其中一个元素被指定为树根

有向图

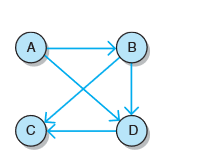
• 有向图也称双向图，是一种边为有序顶点对的图，边（A,B）和（B,A）是不同的有向边
  

• 有向图的路径是连接两个顶点的有向边序列。路径ABD与路径DBA是不同的

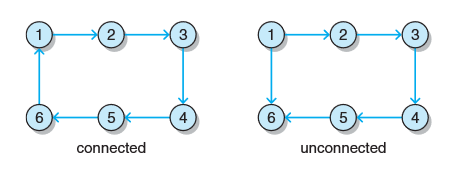
• 若有向图中任意两个顶点之间都存在一条路径，则认为该有向图是连通的。下图中第一个图是连通的，第二个图不是，因为没有任何路径能从其它顶点游历到1，也不能从6出发游历任何其他顶点
  

• 如果有向图中没有环路，且有一条从A到B的边，那么就可以把A安排在顶点B之前，这种排列得到的顶点次序称为拓扑序

• 有向树是一种指定了一个元素作为树根的有向图，该图具有如下属性：

  • 不存在其他顶点到树根的连接
  • 每个非树根元素恰好有一个连接
  • 树根到每个其它顶点都有一条路径

网络

• 网络又称为加权图，是一种每条边都带有权重或代价的图
• 加权图中的路径权重是该路径各边权重之和
• 用三元组表示每条边，包括起始顶点、终止顶点和权重。对于有向图来说，必须包含每个有向连接的三元组

常用的图算法

• 遍历

  • 广度优先遍历（BFS）：类似于树的层次遍历，使用队列和无序列表
  • 深度优先遍历（DFS）：类似于树的前序遍历，使用栈和无序列表

• 测试连通性

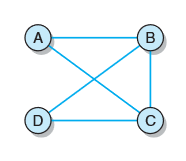
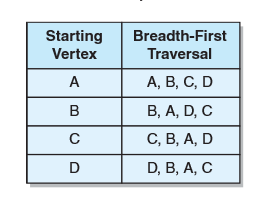
  • 简单解释：在一个含有n个顶点的图中，当且仅当对每个顶点v，从v开始的广度优先遍历的resultList大小都是n，则该图就是连通的。例如

  无向连通图及以每个顶点为起点的广度优先遍历
  
  
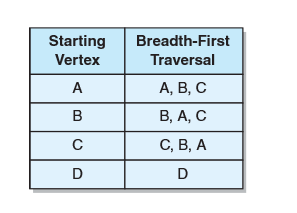
  无向非连通图及以每个顶点为起点的广度优先遍历
  
  

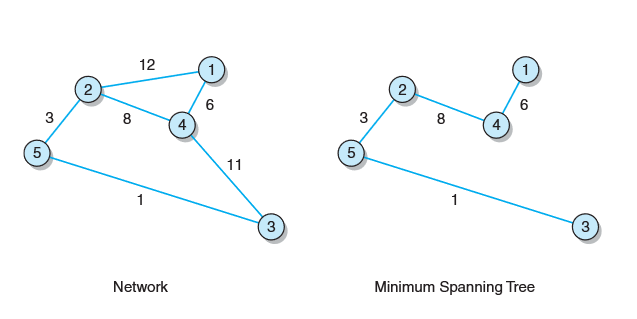
• 最小生成树

  • 生成树是一棵含有图中所有顶点和部分边（但可能不是所有边）的树。
  • 由于树也是图，有些图本身就是一棵生成树，这时该图的唯一生成树将包含所有边。
  • 最小生成树（保持图连通的最少边）（生成树不是唯一的）边的权重总和小于或等于同一图中其他任何一棵生成树的权重总和
  • 最小生成树集合包括n个点和n-1条边。且没有回路。
  • 最小生成树生成过程：从网络中任意选取一个起始顶点，并添加到最小生成树中，然后将所有含起始顶点的边按照权重次序添加到minheap中（如果处理的是有向网络，则只会添加那些以这个特定顶点为起点的边），接着从minheap中取出最小边，并与新顶点添加到最小生成树中。往minheap中添加所有含该新顶点且另一顶点尚不在最小生成树中的边。继续这一过程，直到最小生成树含有原始图中的所有顶点（或minheap为空）时结束。
    

• 判断最短路径

  • 两顶点之间最小边数
    • 在编历时记录从起始顶点到本顶点的路径长度，以及路径中作为本顶点前驱的那个顶点。并当抵达目标顶点时循环终止，最短路径长度就是得到的路径长度加1
  • 加权图的最便宜路径
    • 使用minheap或优先队列来存储顶点，基于总权重衡量顶点对，每个顶点都必须存储该顶点的标签（本顶点之前最便宜的路径权重及路径上本顶点的前驱），从minheap取出顶点的时候，会权衡顶点对，如果未按由小到大取出顶点，则会更新路径

图的实现策略

• 邻接列表

  • 用类似于链表的动态结点来存储每个结点带有的边。这种链表称为邻接列表
  • 对网络或加权图来说，每条边会存储成一个含权重的三元组；对无向图而言，边（A,B）会同时出现在顶点A和顶点B的邻接列表中

• 邻接矩阵

  • 可以用集合储存边
  • 用称为邻接矩阵的二维数组存储顶点，每个单元表示两个顶点的交接情况，由表示是否连通的布尔值表示

  无向图的邻接矩阵
  
  因为是无向图，所以该矩阵沿对角线对称，只需给出一侧即可
  有向图的邻接矩阵
  
  邻接矩阵也可以用于网络或加权图，只需要在矩阵的各个单元中存储一个代表边权重的对象，没有边的单元为null

• 用邻接矩阵实现无向图

  • addEdge方法：使用getIndex方法定位索引并调用addEdge方法进行赋值
  • addVertex方法：往图中添加一个顶点包括在数组的下一个可用位置添加该顶点，把邻接矩阵中所有恰当的位置都设置成false
  • expandCapacity方法：不仅扩展顶点数组并把已有顶点复制到新数组中，而且还必须扩展邻接列表的容量并把旧内容复制到新列表中

教材学习中的问题和解决过程

• 问题一：广度优先遍历和深度优先遍历的实现过程及其原理

• 问题一解决：通过查找资料其过程可认为：

  广度优先遍历（使用一个队列）：

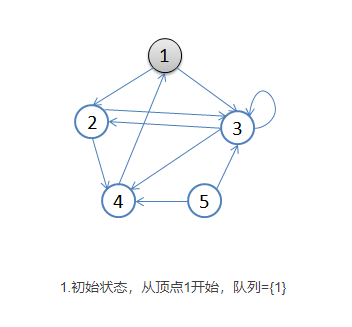
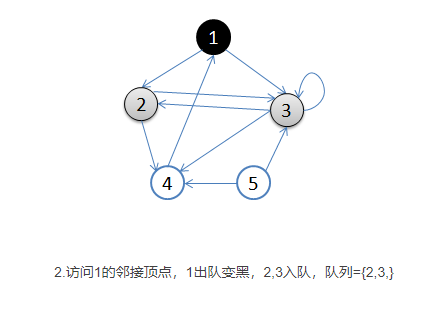
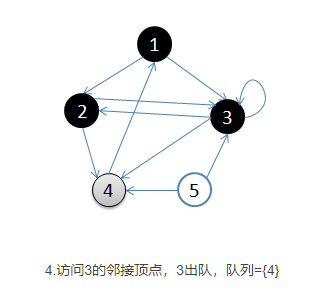
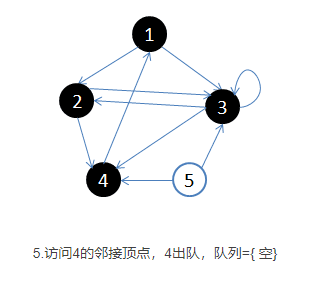
  • 首先选择一个顶点作为起始顶点，让起始顶点进入队列中，并将其染成灰色（visited），其余顶点为白色。
  • 开始循环：从队列首部选出一个顶点，添加到resultList末端（涂黑），并找出所有与之邻接的顶点，放入队列尾部（涂灰），没访问过的顶点是白色。然后再次取出新的起始顶点涂黑放入resultList中，如此循环。如果顶点的颜色是灰色，表示已经发现并且放入了队列，如果顶点的颜色是白色，表示还没有发现。
  • 基本就是出队的顶点变成黑色，在队列里的是灰色，还没入队的是白色。

  
  
  
  
  
  深度优先遍历（使用栈）：

  • 其总体思想为：访问顶点v，依次从v的未被访问的邻接点出发，到一条路径的尽头时，将其入栈返回上一个顶点，若其有其他孩子，继续向下。直到所有顶点都被访问。

  

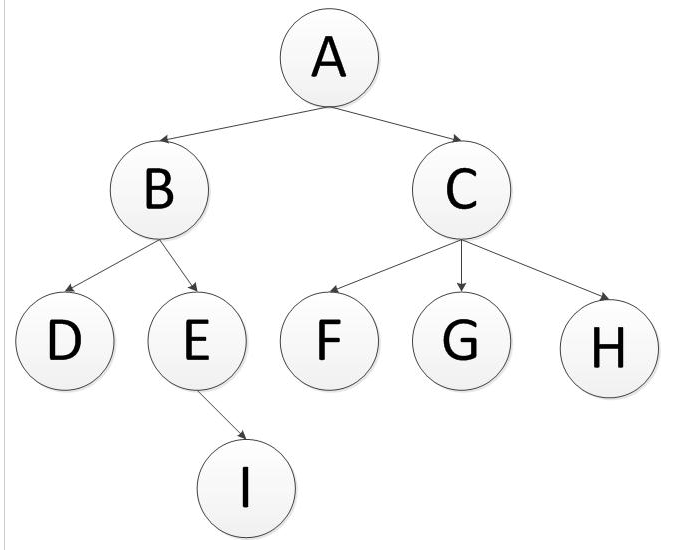
  过程为：

  • 先往栈中压入右节点，再压左节点，这样出栈就是先左节点后右节点了
  • 首先将顶点A压入栈中，stack（A）
  • 将A弹出，进入无序列表中，同时将v的右孩子B和左孩子C压入栈中，此时左孩子在栈的顶部，stack（B,C）
  • 将B顶点弹出，同时将B的子顶点E，D压入栈中，此时D在栈的顶部，stack（D,E,C）
  • 将D顶点弹出，没有子顶点压入,此时E在栈的顶部，stack（E，C）
  • 将E顶点弹出，同时将E的子顶点I压入，stack（I,C）
  • 依次往下，最终遍历完成

  两者之间唯一不同之处是：深度优先遍历使用栈而不是队列来管理遍历

• 问题二：图的邻接列表较难理解

• 问题二解决：邻接列表是对每个顶点建立一个链表，表示以改顶点为起点的所有顶点。通过访问一个顶点的链表即可得出该顶点的所有边。由此也可也得出以改顶点为起点的一条路径。
  有向图：
  
  
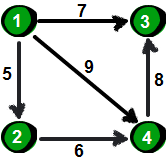
  一共有1234四个顶点，所以建立四个顶点，以1为起点的有234，以2为起点的只有4，以3为起点的没有，以4为起点的只有3。
  无向图：
  
  
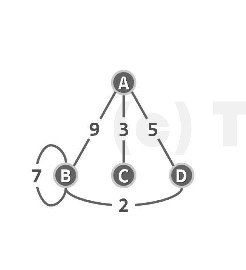
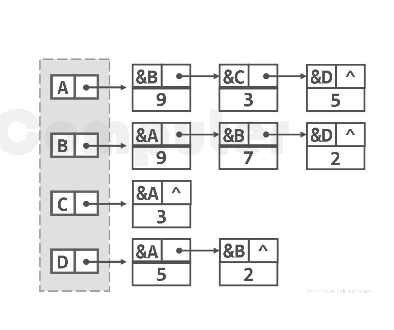
  一共有ABCD四个顶点，建立4个链表。A顶点连接的边是BCD，与B顶点连接的是ABD，与C顶点连接的只有A，与D顶点连接的是AB。

代码调试中的问题和解决过程

• 问题一：在iteratorBFS方法中，

   if (!indexIsValid(startIndex))
          return resultList.iterator();
  

  不清楚iterator方法的作用

• 问题一解决：首先，这个方法的作用是为了使类可迭代，使类迭代需要有以下几步：

  • 在类声明中加入implements Iterable，对应的接口为（即java.lang.Iterator）

    public interface Iterable<Item>{
        Iterator<Item> iterator();
    }
    

  • 在类中实现iterator()方法，返回一个自己定义的迭代器Iterator

    public Iterator<Item> iterator(){
        //如果需要逆序遍历数组，自定义一个逆序迭代数组的迭代器
         return new ReverseArrayIterator();
    }
    

  • 在类中设置内部类（如private class ReverseArrayIterator() ），内部类声明中加入implements Iterator，对应的接口为（即java.util.Iterator）

    public interface Iterator {  
    

　 　boolean hasNext();
　 　Object next();
　 　void remove();
}
```
这些是在第四周中学到过的，比如ArrayList类，完全符合以上步骤。
在这里，由于索引无效，必须要返回一个相同类型的值，实际上就是空的。

• 问题二：对广度优先遍历代码的理解

• 问题二解决：见注释

  private Iterator<T> iteratorBFS(int startIndex) {
      Integer x;
      QueueADT<Integer> traversalQueue = new LinkedQueue<Integer>();
      UnorderedListADT<T> resultList = new ArrayUnorderedList<T>();
      //索引无效，返回空
      if (!indexIsValid(startIndex))
          return resultList.iterator();
      boolean[] visited = new boolean[maxCount];
      //把所有顶点设为false，白色
      for (int i = 0; i < maxCount; i++)
          visited[i] = false;
      //进入队列的为true，即访问过的，灰色
      traversalQueue.enqueue(startIndex);
      visited[startIndex] = true;
      while (!traversalQueue.isEmpty()) {
          //出队列涂黑存入resultList中
          x = traversalQueue.dequeue();
          resultList.addToRear((T) nodelist.get(x).getElement());
          //如果进入resultList的顶点还有相邻的未访问过的顶点，将其涂灰入队
          for (int i = 0; i < maxCount; i++) {
              if (hasEdge(x, i) && !visited[i]) {
                  traversalQueue.enqueue(i);
                  visited[i] = true;
                  Int++;
              }
          }
      }
      return new GraphIterator(resultList.iterator());
      }
  

• 问题三：最短路径的代码理解，不知道iteratorShortestPathIndices方法和iteratorShortestPath方法的联系和区别。

• 问题三解决：iteratorShortestPathIndices方法构建最短路径中顶点集合的迭代器，然后iteratorShortestPath方法获取迭代器并输出构成最短路径的结点。

  • iteratorShortestPath方法

  //最短路径的顶点集
  private Iterator<T> iteratorShortestPath(int startIndex, int targetIndex)
  {
      UnorderedListADT<T> resultList = new ArrayUnorderedList<T>();
      //如果索引值都无效，返回空
      if (!indexIsValid(startIndex) || !indexIsValid(targetIndex))
          return resultList.iterator();
      //it表示构成startindex和targetindex之间最短路径的顶点集，并存储在resultlist链表中，获取结点集合的迭代器对象
      Iterator<Integer> it = iteratorShortestPathIndices(startIndex, targetIndex);
      while (it.hasNext())
          resultList.addToRear((T)nodelist.get(((Integer)it.next())).getElement());
      return new GraphIterator(resultList.iterator());
  }
  

  • iteratorShortestPathIndices方法，构建从开始到结束的节点集合的迭代器对象

  //找到最短路径的顶点值
  private Iterator<Integer> iteratorShortestPathIndices(int startIndex, int targetIndex)
  {
      int index = startIndex;
      int[] pathLength = new int[maxCount];//路径长度数组
      int[] predecessor = new int[maxCount];//前驱结点
      QueueADT<Integer> traversalQueue = new LinkedQueue<Integer>();
      UnorderedListADT<Integer> resultList = new ArrayUnorderedList<Integer>();
      //如果索引无效或起始终点为同一索引，返回空
      if (!indexIsValid(startIndex) || !indexIsValid(targetIndex) || (startIndex == targetIndex))
          return resultList.iterator();
      boolean[] visited = new boolean[maxCount];//访问过为true，染灰
      //先标记为都没访问过，染白
      for (int i = 0; i < maxCount; i++)
          visited[i] = false;
      //将起始值入队标为访问过，染灰
      traversalQueue.enqueue(Integer.valueOf(startIndex));
      visited[startIndex] = true;
      pathLength[startIndex] = 0;//路径长度为0
      predecessor[startIndex] = -1;//前驱结点为-1位置
      //如果还有访问过的灰色，并且未找到目标索引
      while (!traversalQueue.isEmpty() && (index != targetIndex))
      {
          index = (traversalQueue.dequeue()).intValue();//出队列染黑，index储存其元素值
          //如果有其他结点与index有联系却没有被访问过的，入队染灰
          for (int i = 0; i < maxCount; i++)
          {
              if (hasEdge(index,i) && !visited[i])
              {
                  pathLength[i] = pathLength[index] + 1;//长度加一
                  predecessor[i] = index;//index为其前驱结点，predecessor中存储最短路径顶点
                  traversalQueue.enqueue(Integer.valueOf(i));//进队染灰
                  visited[i] = true;
              }
          }
      }
      //如果index不是目标索引，返回空
      if (index != targetIndex)
          return resultList.iterator();
      StackADT<Integer> stack = new LinkedStack<Integer>();
      index = targetIndex;
      stack.push(Integer.valueOf(index));//目标索引入栈
      do
      {//index不是起始索引值的元素值时，index表示其前驱结点的元素值，将结点的值依次入栈
          index = predecessor[index];
          stack.push(Integer.valueOf(index));
      } while (index != startIndex);
      while (!stack.isEmpty())
          resultList.addToRear(((Integer)stack.pop()));//栈不为空时，弹出结点添加到resultlist链表
      return new GraphIndexIterator(resultList.iterator());//resultlist中储存的就是最短路径的顶点集
  }
  

• 问题四：出现从未遇到过的异常：Exception in thread "main" java.lang.OutOfMemoryError: Java heap space
  

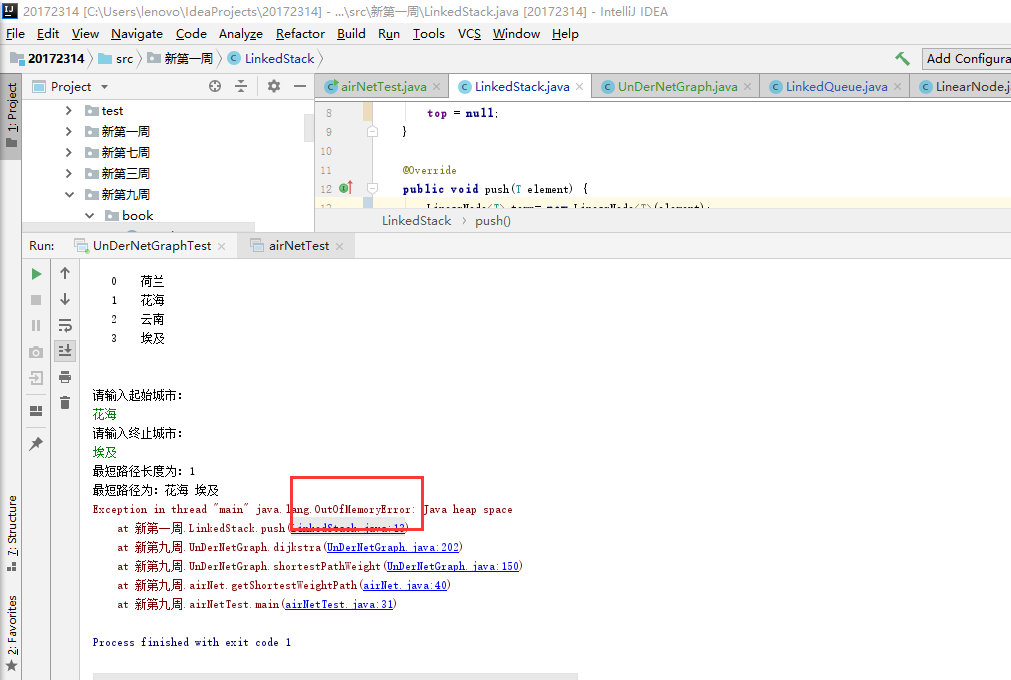
• 问题四解决：有三种可能导致此类错误的情况：

  • 真实的存在内存泄漏
  • 没有为应用程序提供足够多的内存，这种情况下，可以增加JVM堆可用空间大小，或者减少程序所需内存量
  • 程序中无心的对象引用保持，使得没有明确的释放对象，以致于堆增长再增长，直到没有额外的空间。
    网上的解决办法：

  选中被运行的类，点击菜单‘run->run...’，选择(x)=Argument标签页下的vm arguments框里
  输入 -Xmx800m, 保存运行。

  但我没怎么明白具体操作，我认为我的错误可能是第三种情况，于是把第一周中inkedStack方法检查了一下，发现方法size,isEmpty,和toString不完善，在其他方法的条件中调用时就有可能出错，修改之后问题解决。

代码托管

上周考试错题总结

无

结对及互评

• 谭鑫20172305：谭鑫的博客中最突出的就是他的扩展学习很多，比如Tarjan算法是我没有了解的，可以说很用心了，博客总结的一直很详细，小小的建议就是希望解释的时候可以分一下层次，一大段一大段的有点难阅读(o´ω`o)ﾉ

• 王禹涵20172323：王禹涵的博客整体很好，及哦啊才问题总结详细，有一个问题就是不太明白代码问题二。

其他

关于图的概念有逻辑性，容易理解，但是问题还是在代码理解上，我觉得Java学习不能停留在知识表面，要深入理解代码，并学会构造才是最终目的。

学习进度条

	代码行数（新增/累积）	博客量（新增/累积）	学习时间（新增/累积）
目标	5000行	30篇	400小时
第一周	0/0	1/1	8/8
第二周	1163/1163	1/2	15/23
第三周	774/1937	1/3	12/50
第四周	3596/5569	2/5	12/62
第五周	3329/8898	2/7	12/74
第六周	4541/13439	3/10	12/86
第七周	1740/15179	1/11	12/97
第八周	5947/21126	1/12	12/109
第九周	7968/29094	2/14	12/121

参考

• 图的邻接表的实现