要是没学过高等数学的积分怎么办呢?可以求助于自适应辛普森法。
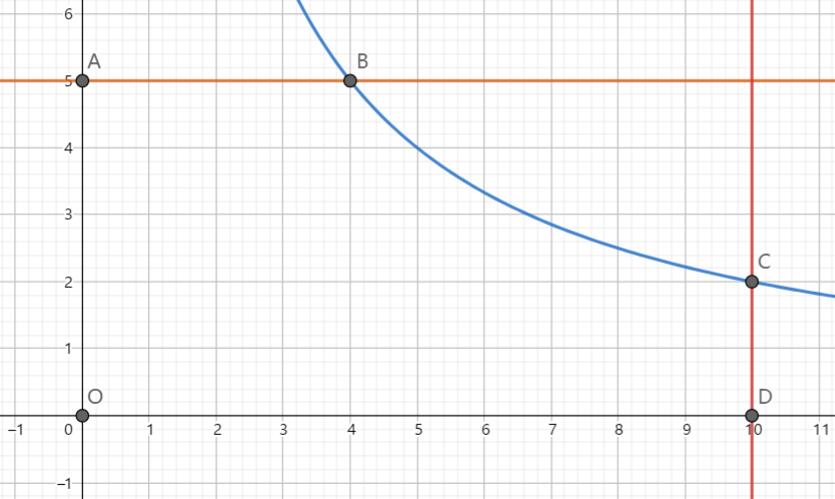
容易发现其实这个图形是对称的,我们只要求第一象限就可以了,第一象限如上图。
由于取点是在面积内等概率的,由高中的几何概型可知,所求概率为:
1.当S<=ab,则双曲线与矩形有交点,概率的分子为上图中 矩形面积 减去 OABCD面积,分母为矩形面积。
2.当S>ab,则概率为1。
所求的面积为双曲线 (y=frac{S}{x}) 在 直线 (y=b) 下,从 (0) 到 (a) 的积分。
表述为 (F(x)=min(frac{S}{x},b)) 。
然后我们套一个自适应辛普森法求积分就可以了。
(不可能是省选的难度,连我都会)
在F中有对无穷小的特判,去掉的话不会有什么问题,但是总感觉能避免除以0的RE挺好的。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
double seps=1e-12;
double a,b,S;
double F(double x) {
//需要积分的函数F
/*if(x<1e-8)
return b;*/
return min(b,S/x);
}
double simpson(double l,double r) {
double mid=(l+r)/2;
return (F(l)+4*F(mid)+F(r))*(r-l)/6;
}
double asr(double l,double r,double A) {
double mid=(l+r)/2;
double L=simpson(l,mid),R=simpson(mid,r);
if(fabs(L+R-A)<=15*seps)
return L+R+(L+R-A)/15.0;
return asr(l,mid,L)+asr(mid,r,R);
}
double asr(double l,double r) {
return asr(l,r,simpson(l,r));
}
int main() {
int t;
cin>>t;
while(t--) {
cin>>a>>b>>S;
double p=0;
if(S+(-1e-10)<=0)
p=1.0;
else if(S+(1e-10)>=a*b) {
p=0.0;
} else {
p=1.0-asr(0,a)/(a*b);
}
p*=100.0;
printf("%.6f%
",p);
}
}