这大概是我看的最好懂的KMP算法讲解了,不过我还只弄懂了大概思想,算法实现我到时候用java实现一遍
出处:知乎 https://www.zhihu.com/question/21923021/answer/281346746
有些算法,适合从它产生的动机,如何设计与解决问题这样正向地去介绍。但KMP算法真的不适合这样去学。最好的办法是先搞清楚它所用的数据结构是什么,再搞清楚怎么用,最后为什么的问题就会有恍然大悟的感觉。我试着从这个思路再介绍一下。大家只需要记住一点,PMT是什么东西。然后自己临时推这个算法也是能推出来的,完全不需要死记硬背。
KMP算法的核心,是一个被称为部分匹配表(Partial Match Table)的数组。我觉得理解KMP的最大障碍就是很多人在看了很多关于KMP的文章之后,仍然搞不懂PMT中的值代表了什么意思。这里我们抛开所有的枝枝蔓蔓,先来解释一下这个数据到底是什么。
对于字符串“abababca”,它的PMT如下表所示:

就像例子中所示的,如果待匹配的模式字符串有8个字符,那么PMT就会有8个值。
我先解释一下字符串的前缀和后缀。如果字符串A和B,存在A=BS,其中S是任意的非空字符串,那就称B为A的前缀。例如,”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”},我们把所有前缀组成的集合,称为字符串的前缀集合。同样可以定义后缀A=SB, 其中S是任意的非空字符串,那就称B为A的后缀,例如,”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”},然后把所有后缀组成的集合,称为字符串的后缀集合。要注意的是,字符串本身并不是自己的后缀。
有了这个定义,就可以说明PMT中的值的意义了。PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。例如,对于”aba”,它的前缀集合为{”a”, ”ab”},后缀 集合为{”ba”, ”a”}。两个集合的交集为{”a”},那么长度最长的元素就是字符串”a”了,长 度为1,所以对于”aba”而言,它在PMT表中对应的值就是1。再比如,对于字符串”ababa”,它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”},它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}, 两个集合的交集为{”a”, ”aba”},其中最长的元素为”aba”,长度为3。
好了,解释清楚这个表是什么之后,我们再来看如何使用这个表来加速字符串的查找,以及这样用的道理是什么。如图 1.12 所示,要在主字符串"ababababca"中查找模式字符串"abababca"。如果在 j 处字符不匹配,那么由于前边所说的模式字符串 PMT 的性质,主字符串中 i 指针之前的 PMT[j −1] 位就一定与模式字符串的第 0 位至第 PMT[j−1] 位是相同的。这是因为主字符串在 i 位失配,也就意味着主字符串从 i−j 到 i 这一段是与模式字符串的 0 到 j 这一段是完全相同的。而我们上面也解释了,模式字符串从 0 到 j−1 ,在这个例子中就是”ababab”,其前缀集合与后缀集合的交集的最长元素为”abab”, 长度为4。所以就可以断言,主字符串中i指针之前的 4 位一定与模式字符串的第0位至第 4 位是相同的,即长度为 4 的后缀与前缀相同。这样一来,我们就可以将这些字符段的比较省略掉。具体的做法是,保持i指针不动,然后将j指针指向模式字符串的PMT[j −1]位即可。
简言之,以图中的例子来说,在 i 处失配,那么主字符串和模式字符串的前边6位就是相同的。又因为模式字符串的前6位,它的前4位前缀和后4位后缀是相同的,所以我们推知主字符串i之前的4位和模式字符串开头的4位是相同的。就是图中的灰色部分。那这部分就不用再比较了。


具体的程序如下所示:int KMP(char * t, char * p)
{
int i = 0;
int j = 0;
while (i < strlen(t) && j < strlen(p))
{
if (j == -1 || t[i] == p[j])
{
i++;
j++;
}
else
j = next[j];
}
if (j == strlen(p))
return i - j;
else
return -1;
}
好了,讲到这里,其实KMP算法的主体就已经讲解完了。你会发现,其实KMP算法的动机是很简单的,解决的方案也很简单。远没有很多教材和算法书里所讲的那么乱七八糟,只要搞明白了PMT的意义,其实整个算法都迎刃而解。
现在,我们再看一下如何编程快速求得next数组。其实,求next数组的过程完全可以看成字符串匹配的过程,即以模式字符串为主字符串,以模式字符串的前缀为目标字符串,一旦字符串匹配成功,那么当前的next值就是匹配成功的字符串的长度。
具体来说,就是从模式字符串的第一位(注意,不包括第0位)开始对自身进行匹配运算。 在任一位置,能匹配的最长长度就是当前位置的next值。如下图所示。
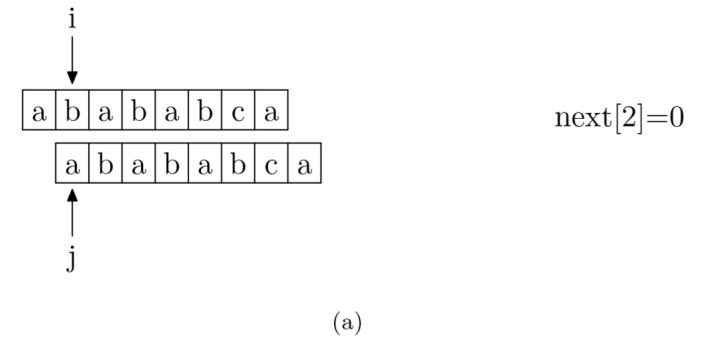




求next数组值的程序如下所示:
void getNext(char * p, int * next)
{
next[0] = -1;
int i = 0, j = -1;
while (i < strlen(p))
{
if (j == -1 || p[i] == p[j])
{
++i;
++j;
next[i] = j;
}
else
j = next[j];
}
}
至此,KMP算法就全部介绍完了.
java实现
public class Main {
public static void main(String[] args) throws Exception{
int k = KMP("aababababca","abababca",getNext("abababca"));
System.out.println(k);
}
/**
* KMP算法
* @return 匹配的第一个位置
* @param next next数组
* @param modelString 模式串
* @param mainString 主串
* */
public static int KMP(String mainString,String modelString,int[] next){
int i = 0;
int j = 0;
while (i<mainString.length()&&j<modelString.length()){
if(-1==j||mainString.charAt(i) == modelString.charAt(j)){
i++;
j++;
}else {
//不相等,滑动
j = next[j];
}
}
if(j==modelString.length()){
//如果最后j到达模式串的尾部,则说明匹配上了
return i - j;
}else {
return -1;
}
}
/**
* @param modelString 模式字符串
* 求next数组
* */
public static int[] getNext(String modelString){
int[] next = new int[100];
next[0] = -1;
int i = 0;
int j = -1;
while (i<modelString.length()){
if(j==-1||modelString.charAt(i)==modelString.charAt(j)){
//相等的情况
i++;
j++;
next[i] = j;
}
else {
j = next[j];
}
}
return next;
}
}