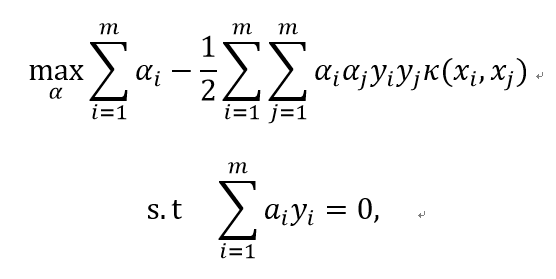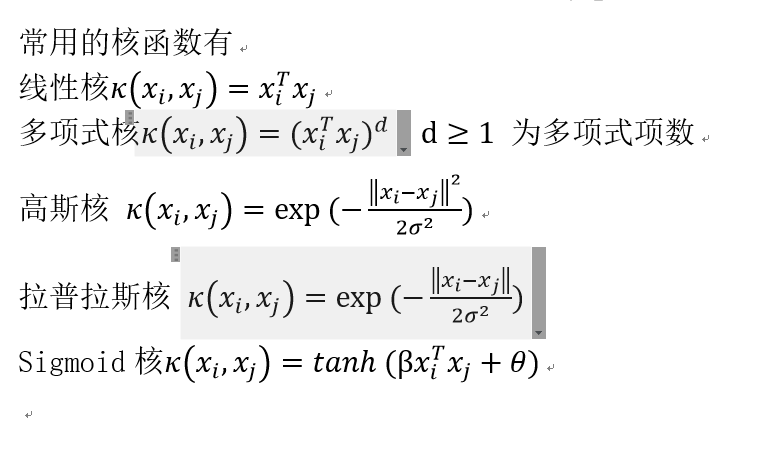支持向量机是一种二分类模型,它的基本思想就是基于训练集D在样本空间中找到一个划分超平面,将不同类别的样本分开。但是,能将训练样本分开的划分超平面可能有很多,因此,我们应该致力于找位于两类训练样本“正中间”的划分超平面,因为这样的划分超平面对训练样本局部扰动的容忍性最好。支持向量机学习算法主要有三种,有:线性可分支持向量机,线性支持向量机和非线性支持向量机。当训练数据线性可分时,通过硬间隔最大化,学习一个线性分类器,又称硬间隔支持向量机;当训练数据近似线性可分但不是完全线性可分时,通过软间隔最大化,学习一个线性分类器,即线性支持向量机;当训练数据线性不可分时,通过核技巧及软间隔最大化,学习非线性支持向量机。
划分超平面可以通过以下线性方程来描述
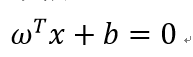
假设超平面能将所有训练样本正确分类,则有
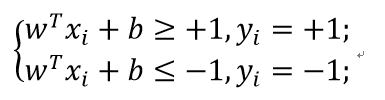
上式中使等式成立的训练样本被称为支持向量。由此可知,两个异类支持向量到超平面的距离之和是
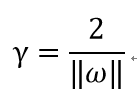
支持向量机算法的计算目标就是要找到符合条件的具有最大间隔的划分超平面,这可以写成一个最优化问题即
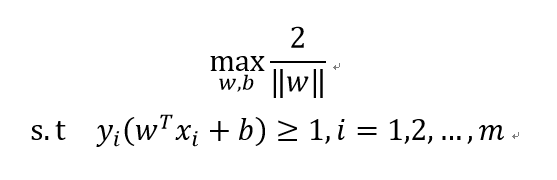
上面问题重写即支持向量机的基本型:
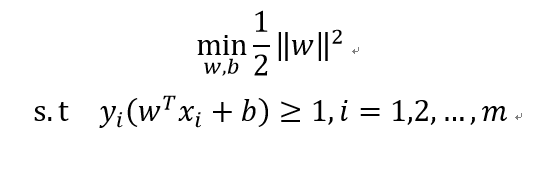
经过数学推导,我们可以得到上式的对偶形式
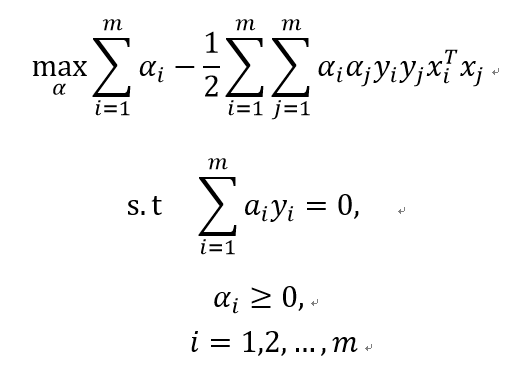
求得 后,可以得到
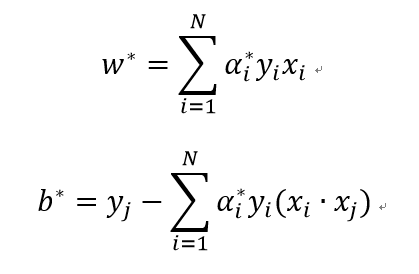
以上是支持向量机中最简单的一种,即样本点可以由一个空间平面完全分割开。这是一种“硬间隔”。有的时候,训练样本点不能由一个空间平面完全分开,即一种“软间隔”,这时需要需要对上述公式做出一点修改即可。
修改后的公式如下
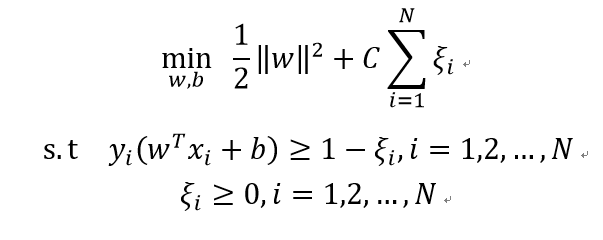
解法与上面类似。
以上解决的都是线性问题。有时候,训练数据并不能由一个空间平面完全分开,而是可以由一个其他形式的面分开,此时就是非线性问题。此时用核技巧往往可以解决问题。
此时的对偶函数公式可以写作