古代猪文

数论综合，考察代码能力（其实是脑子）……

首先分析一下其实就是求一个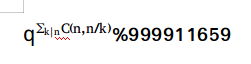（1）。

略微转换一下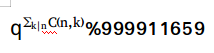（2）。

因为k是n的因子，n/k是n的因子，将两个因子交换位置就可以由（1）得到（2）。

接着就是尝试缩小计算规模的过程。

因为999911659是个素数，由欧拉定理的推论得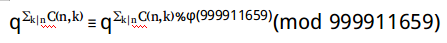：（3）。

那么我们就可以试着去求（4）。

尝试对999911658用唯一分解定理，发现可以拆成2，3，4679，35617。

这四个数是互质的，我们可以利用lucas定理将对2，3，4679，35617的余数分别求出，设为a1,a2,a3,a4。

问题转化为求一个x，使之满足：

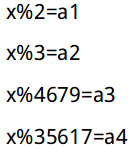
这是一个典型的同余方程组，即：

x是可以用CRT求解的。

最后有了x，有了q，快速幂求一下q^x就是结果了。

下面的代码还是不要看的好，因为求fac和inv那一段特别丑，而且交完oj缩进问题十分严重。

有一个位置一开始打崩了，枚举因子时打成O(n)了，应该是O（sqrt（n））的，和判断素数那个思路差不多。

#include<iostream>
#include<algorithm>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<stack>
#define LL long long 
using namespace std;
LL n,q;
LL read(){
    LL sum=0;int f=1;char x=getchar();
    while(x<'0'||x>'9'){
        if(x=='-') f=-1;
        x=getchar();
    }while(x>='0'&&x<='9'){
        sum=sum*10+x-'0';
        x=getchar();
    }
    return sum*f;
    
}
LL p[6]={0,2,3,4679,35617};
LL fac[10][50050],inv[10][50050];
LL a[6];
LL qpow(LL x,LL k,LL mod){
    LL ans=1;
    for(;k;k>>=1,x=x*x%mod)
        if(k&1)
            ans=ans*x%mod;
    return ans;
}
void exgcd(LL a,LL b,LL &x,LL &y){
    if(!b){
        x=1;y=0;
        return;
    }
    exgcd(b,a%b,x,y);
    LL t=x;
    x=y;
    y=t-a/b*x;
    return ;
}
LL CRT(){
    LL ans=0,x,y;
    for(int i=1;i<=4;i++){
        exgcd(999911658/p[i],p[i],x,y);
        ans=(ans+a[i]*999911658/p[i]*x)%999911658;
    }return (ans+999911658)%999911658;
}
LL C(LL n,LL m,int i){
    if(m>n) return 0;
    return ((fac[i][n]*inv[i][m])%p[i])*inv[i][n-m]%p[i];
}
LL lucas(LL n,LL m,int i){
    if(m==0) return 1;
    return C(n%p[i],m%p[i],i)*lucas(n/p[i],m/p[i],i)%p[i];
}
void pre(){
    fac[1][0]=fac[2][0]=fac[3][0]=fac[4][0]=1;
    fac[1][1]=1;
    for(int i=1;i<=2;i++) fac[2][i]=fac[2][i-1]*i%p[2];
    for(int i=1;i<=4678;i++) fac[3][i]=fac[3][i-1]*i%p[3];
    for(int i=1;i<=35616;i++) fac[4][i]=fac[4][i-1]*i%p[4];
    inv[1][1]=qpow(fac[1][1],p[1]-2,p[1]);
    inv[2][2]=qpow(fac[2][2],p[2]-2,p[2]);
    inv[3][4678]=qpow(fac[3][4678],p[3]-2,p[3]);
    inv[4][35616]=qpow(fac[4][35616],p[4]-2,p[4]);
    for(int i=35616;i>=1;i--)
        inv[4][i-1]=inv[4][i]*i%p[4];
    for(int i=4678;i>=1;i--)
        inv[3][i-1]=inv[3][i]*i%p[3];
    for(int i=2;i>=1;i--)
        inv[2][i-1]=inv[2][i]*i%p[2];
    for(int i=1;i>=1;i--)
        inv[1][i-1]=inv[1][i]*i%p[1];

}
int main(){
    n=read();q=read();
    if(q%999911659==0){
        puts("0");
        return 0;
    }
    pre();
    for(int i=1;i*i<=n;i++){
        if(n%i==0){
            for(int j=1;j<=4;j++)
                a[j]=(a[j]+lucas(n,i,j))%p[j];
            if(i*i!=n)
                for(int j=1;j<=4;j++)
                    a[j]=(a[j]+lucas(n,n/i,j)%p[j]);
        }
    }
    LL o=CRT();
    printf("%lld
",qpow(q,o,999911659));
    return 0;
}