HDU 6158 笛卡尔定理 几何

LINK

题意：一个大圆中内切两个圆，三个圆两两相切，再不断往上加新的相切圆，问加上的圆的面积和。具体切法看图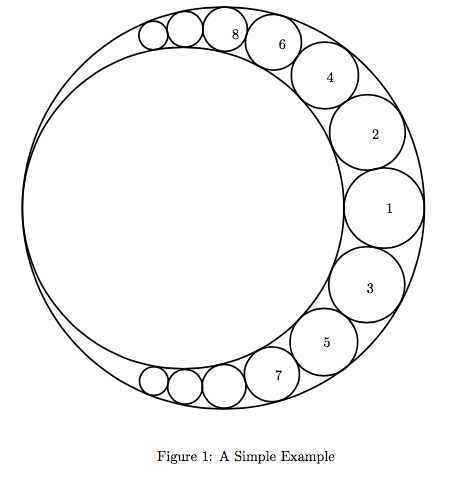

思路：笛卡尔定理：

若平面上四个半径为r1、r2、r3、r4的圆两两相切于不同点，则其半径满足以下结论：

　　　　　　　　　　（1）若四圆两两外切，则

  

　　　　　　　　　　（2）若半径为r1、r2、r3的圆内切于半径为r4的圆中，则

  

显然现在是第二种情况，设弧度为$k$则，$r_1,r_2,r_3,r_4$的弧度为$k_1,k_2,k_3,k_4$,其中$r_4$是下个我们要求的圆的半径，显然我们已知前三个圆，第四个圆可由递推求得。

那么，化简公式到这步$k_4^2 - {color{red}{2(k_2 + k_3 - k_1)k_4}} - [2k_{2}k_{3} + 2k_{1}(k_2 + k_3) + k_2^2 + k_3^2 + k_1^2] = 0$ 

当$i>=4$时这里可以发现$k_i$的两个解就是$r_{i-1}$两侧的两个圆的弧度，其中一个圆是上一步得到的圆，那么我们可以使用伟达定理,即$k_{i} + k_{i-2} = 2(k_2 + k_{i-1} - k_1)k_i$，再移项得到递推式，除了第一个圆，每次画上下对称的两个圆，注意由于$n<=10^7$，如果全部递推会超时，所以还要剪掉面积太小的部分...这部分精度还不能太低..

老实说，以后再出纯数学题，照样还是做不来的，笛卡尔定理还是看了icpccamp上的题解才知道的..就当积累姿势好了。

说起来这道题在这里就有一道基本一模一样的数学题(例3)....

/** @Date    : 2017-08-21 15:31:07
  * @FileName: 1009 笛卡尔定理.cpp
  * @Platform: Windows
  * @Author  : Lweleth (SoungEarlf@gmail.com)
  * @Link    : https://github.com/
  * @Version : $Id$
  */
#include <bits/stdc++.h>
#define LL long long
#define PII pair<int ,int>
#define MP(x, y) make_pair((x),(y))
#define fi first
#define se second
#define PB(x) push_back((x))
#define MMG(x) memset((x), -1,sizeof(x))
#define MMF(x) memset((x),0,sizeof(x))
#define MMI(x) memset((x), INF, sizeof(x))
using namespace std;

const int INF = 0x3f3f3f3f;
const int N = 1e5+20;
const double eps = 1e-9;
const double Pi = acos(-1.0);

int main()
{
 	int T;
 	cin >> T;
 	while(T--)
 	{
 		int n;
 		double r1, r2, r3, r4;
 		scanf("%lf%lf", &r1, &r2);
 		scanf("%d", &n);
 		if(r1 < r2) swap(r1, r2);

 		r3 = r1 - r2;
 		double k1 = 1.0000 / r1, k2 = 1.0000 / r2, k3 = 1.0000/r3;
 		double k4 = k2 + k3 - k1;//k4 + k4 = -2(k2 + k3 - k1)/-1;
 		double ans = r3 * r3;

 		n -= 1;
 		while(n > 0)
 		{
 			r4 = 1.0000 / k4;
 			double siz = r4 * r4;
 			if(siz < 1e-13) break; //减枝TLE 1e-9 精度太低
 			ans += siz * 2.0000;
 			double nk = 2.0000 * (k2 + k4 - k1) - k3;//k3 + k5 = 2 * (k2 + k4 - k1)
 			k3 = k4;
 			k4 = nk;
 			n -= 2;
 		}
 		if(n < 0)
 			ans -= r4 * r4;
 		printf("%.5lf
", ans * Pi);
 	}
    return 0;
}