简介:Wiki
通俗地理解,例如有10个年龄不同的人,统计出有8个人的年龄比A小,那A的年龄就排在第9位,用这个方法可以得到其他每个人的位置,也就排好了序。当然,年龄有重复时需要特殊处理(保证稳定性),这就是为什么最后要反向填充目标数组,以及将每个数字的统计减去1。算法的步骤如下:
- 找出待排序的数组中最大和最小的元素
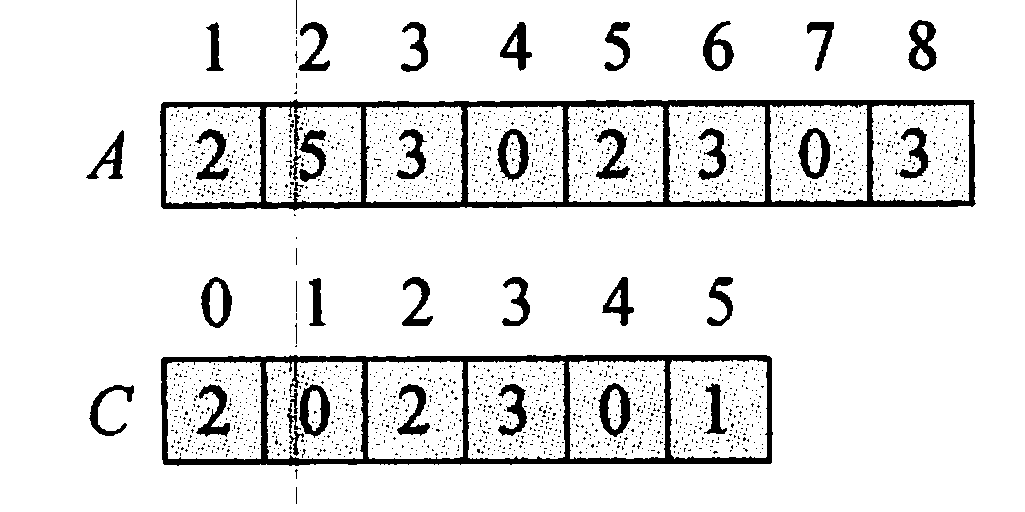
- 统计数组中每个值为{displaystyle i}
的元素出现的次数,存入数组{displaystyle C}
的第{displaystyle i}
项
- 对所有的计数累加(从{displaystyle C}
中的第一个元素开始,每一项和前一项相加)
- 反向填充目标数组:将每个元素{displaystyle i}
放在新数组的第{displaystyle C[i]}
项,每放一个元素就将{displaystyle C[i]}
减去1
计数
加总
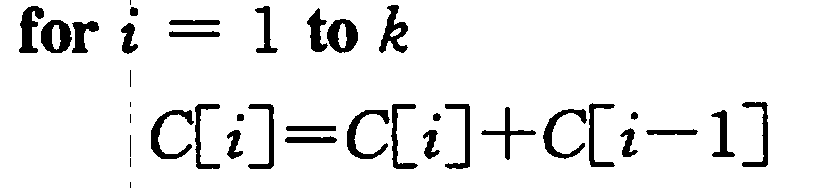
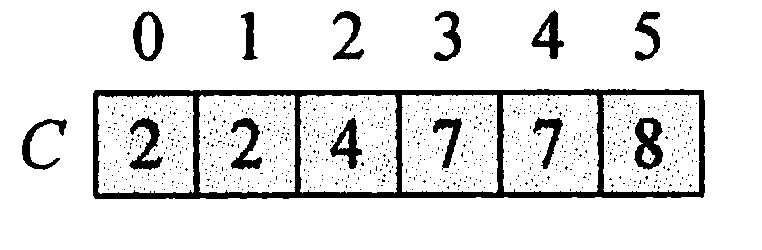
//对每个A[i]值来说,C[A[i]]就是A[i]在输出数组中的最终正确位置(从1起)
//因为有相等元素,所以C[A[i]]的值减1:所以具有稳定性
//稳定性:对两个相同的数来说,在输入数组中先出现的数,在输出数组中也在前面
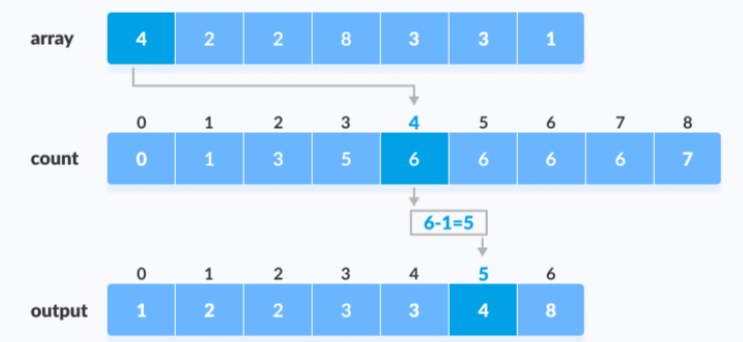
c++ code
1 #pragma once 2 #include<vector> 3 //当k = O(n)时,采用计数排序,运行时间theta(n) 4 //theta(k)+theta(n)+theta(k)+theta(n)=theta(n) 5 std::vector<int> 6 Count_sort(const std::vector<int>& A, const int& k) 7 { 8 std::vector<int> c(k + 1); 9 //计数:theta(k) 10 for (int j = 0;j != A.size(); ++j) 11 ++c[A[j]]; 12 //加总:theta(n) 13 for (int i = 1;i <= k;++i) 14 c[i] += c[i - 1]; 15 //布置:theta(k) 16 std::vector<int> b(A.size()); 17 //:theta(n) 18 for (int i = A.size()-1; i >= 0;--i) 19 //对每个A[i]值来说,C[A[i]]就是A[i]在输出数组中的最终正确位置(从1起) 20 //因为有相等元素,所以C[A[i]]的值减1:所以具有稳定性 21 //稳定性:对两个相同的数来说,在输入数组中先出现的数,在输出数组中也在前面 22 b[--c[A[i]]] = A[i]; 23 return b; 24 }
main.cpp
1 #include<iostream> 2 #include<algorithm> 3 #include<iterator> //ostream_iterator 4 #include"COUNTING_SORT.h" 5 6 using namespace std; 7 8 void print(const vector<int>& v) 9 { 10 ostream_iterator<int> out_iter(cout, " "); 11 copy(v.cbegin(), v.cend(), out_iter); 12 cout << endl; 13 } 14 void CountingSort() 15 { 16 vector<int> v = { 2,5,3,0,2,3,0,3 }; 17 print(v); 18 print(Count_sort(v, *max_element(v.cbegin(), v.cend()))); 19 } 20 int main() 21 { 22 CountingSort(); 23 }