Wiki:
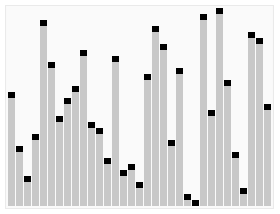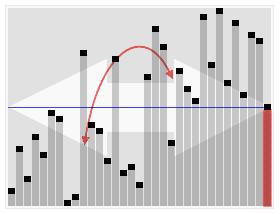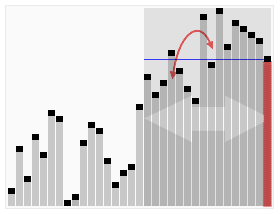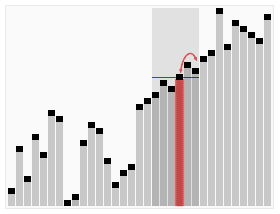
快速选择的总体思路与快速排序一致,选择一个元素作为基准来对元素进行分区,将小于和大于基准的元素分在基准左边和右边的两个区域。不同的是,快速选择并不递归访问双边,而是只递归进入一边的元素中继续寻找。这降低了平均时间复杂度,从O(n log n)至O(n),不过最坏情况仍然是O(n2)。
code
1 #pragma once 2 #include<vector> 3 #include<random> 4 5 int Partiton(std::vector<int>& A, const int p, const int r) 6 { 7 //int 有-1值 8 int i = p - 1; 9 //A[r]是主元不参与划分数组 j != r 10 for (int j = p;j != r;++j) 11 { 12 if (A[j] < A[r]) 13 { 14 ++i; 15 std::swap(A[i], A[j]); 16 } 17 } 18 std::swap(A[i + 1], A[r]); 19 return i + 1; 20 } 21 int Randomized_Partition(std::vector<int>& A, int p, int r) 22 { 23 std::default_random_engine e; 24 std::uniform_int_distribution<unsigned> u(p, r); 25 int i = u(e); 26 std::swap(A[r], A[i]); 27 return Partiton(A, p, r); 28 } 29 30 int Randomized_Select(std::vector<int>& A, const int p, const int r, const int i) 31 { 32 if (p == r) 33 return A[p]; 34 int q = Randomized_Partition(A, p, r); 35 int k = q - p + 1; 36 if (i == k)//i为第i小元素,k为A[p,q]元素个数(小于主元的L array) 37 return A[q];//k i 也行?: 不行以0起始 38 if (i < k) 39 return Randomized_Select(A, p, q - 1, i); 40 else 41 return Randomized_Select(A, q + 1, r, i); 42 43 } 44 int Randomized_Select(std::vector<int>& A, const int i) 45 { 46 int r = A.size() - 1; 47 return Randomized_Select(A, 0, r, i); 48 }