Wiki:二叉查找树(英语:Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于或等于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树
总的来说:《c++ primr 5th》每次看都觉得厉害
1、shared_ptr 是真的香
2、template 友元用的时候在看
3、函数传递:指针形参属于传值(拷贝),shared_ptr引用传递 没必要:动态内存(猜测)
4、cosnt 成员函数适用:不能把this指针 绑定到常量对象(如const double pi = 3.14):return pi;
具体学习到什么 看code注释
1 #pragma once
2 //编译器需要掌握函数模板或模板成员函数的定义:成员函数定义 也在头文件中
3 //成员函数定义在类外使用默认实参 报错:不允许使用默认参数(原因还未知)
4 //原因:非静态数据成员不能作为默认实参:因为它的值本身属于对象的一部分,
5 //这么做的结果是:无法真正提供一个对象以便从中获取成员的值
6
7 /*
8 指针传递:形参是指针的拷贝,两个指针是不同的指针 但是可以间接修改所指向对象的值
9 尽量使用引用传递:避免拷贝的效率和空间
10 尽量使用值初始化:避免多余默认初始化
11 type* & :指向指针的引用 :引用本身不是对象所以不能定义指向引用的指针
12 =运算符在结点上的意义是什么? 指针之间的赋值操作:所以不需要定义赋值运算符不是类之间操作
13 类的行为像指针:共享状态 最好的方法是使用shared_ptr
14 */
15
16 #include<iostream>
17 #include<memory> //shared_ptr
18 template<typename T> class BST;//前置声明:友元所需要
19 template<typename T>
20 //在Tree_Note类内:直接使用模板名而不提供实参:Tree_Note = Tree_Note<T>
21 class Tree_Note
22 {
23 friend class BST<T>;//每个Tree_Note实例将访问权限授予用相同类型实例化的BST
24 public:
25 //构造函数
26 Tree_Note(const T& _key = T())
27 :left(nullptr), right(nullptr), parent(nullptr),key(_key){}
28 /*
29 stack overflow why???
30 答:make_shared 调用Tree_Note构造函数则造成无线循环
31 而用内置已经存在构造函数的则不会 :data(make_shared<vector<string>>()):data = ""
32 :left(std::make_shared<Tree_Note>()),
33 right(std::make_shared<Tree_Note>()), parent(std::make_shared<Tree_Note>()),key(_key) {}
34 */
35 /* 没用上拷贝构造
36 //为了与内置运算符一致:返回指向左侧运算对象的引用:
37 decltype(auto) operator=(std::make_ptr<Tree_Note> right)
38 {//decltype(auto)详见:《Effective Modern C++》P31
39 key = right.key;
40 return maked_shared<Tree_Note>(*this);
41 }
42 */
43 private:
44 T key;
45 std::shared_ptr<Tree_Note> left;
46 std::shared_ptr<Tree_Note> right;
47 std::shared_ptr<Tree_Note> parent;
48 };
49
50 template<typename T>
51 class BST
52 {
53 public:
54 //若root(nullptr) 则:报错访问内存受限
55 BST() :root(nullptr) {} //若使用构造函数则 root.key = 0
56 //中序遍历
57 void Iorder_Tree_Walk(const std::shared_ptr<Tree_Note<T>> x);
58 void Iorder_Tree_Walk() {Iorder_Tree_Walk(root);}
59 //递归查找
60 std::shared_ptr<Tree_Note<T>> Tree_Search(const T& key,const std::shared_ptr<Tree_Note<T>> x);
61 bool Tree_Seach(const T& key)
62 {
63 auto p = Tree_Search(key, root);
64 if (p != nullptr)
65 return true;
66 else
67 return false;
68 }
69 //迭代查找:对于大多数计算机,迭代版本的效率要高的多 :调用函数开销
70 std::shared_ptr<Tree_Note<T>> Iterative_Tree_Search(const T& key,std::shared_ptr<Tree_Note<T>> x);
71 bool Iterative_Tree_Search(const T& key)
72 {
73 auto p = Iterative_Tree_Search(key, root);
74 if (p != nullptr)
75 return true;
76 else
77 return false;
78 }
79
80 //最小值
81 std::shared_ptr<Tree_Note<T>> Tree_Minimum(std::shared_ptr<Tree_Note<T>> x);
82 T Tree_Minimum()
83 {
84 auto p = Tree_Minimum(root);
85 return p->key;
86 }
87 //最大值
88 std::shared_ptr<Tree_Note<T>> Tree_Maximum(std::shared_ptr<Tree_Note<T>> x);
89 T Tree_Maximum()
90 {
91 auto p = Tree_Maximum(root);
92 return p->key;
93 }
94
95 //后继和前驱:最接近(大小)该节点的大、小节点
96 std::shared_ptr<Tree_Note<T>> Tree_Successor(std::shared_ptr<Tree_Note<T>> x);
97 std::shared_ptr<Tree_Note<T>> Tree_Predecessor(std::shared_ptr<Tree_Note<T>> x);
98
99 //插入和删除
100 void Tree_Insert(std::shared_ptr<Tree_Note<T>> z); //当为空树是z要赋值给root 而root不能是const,所以z不是const
101 void Tree_Insert(const T& key)
102 {
103 auto z = std::make_shared<Tree_Note<T>>(key);
104 Tree_Insert(z);
105 }
106 void Tree_Delete(std::shared_ptr<Tree_Note<T>> z);
107 void Tree_Delete(const T& key)
108 {
109 auto z = Iterative_Tree_Search(key, root);
110 if (z == nullptr)
111 std::cerr << "nodata!";
112 Tree_Delete(z);
113 }
114 private:
115 std::shared_ptr<Tree_Note<T>> root;
116 //移植节点 :u = v(不包括左右孩子)
117 void Transplant(std::shared_ptr<Tree_Note<T>> u, std::shared_ptr<Tree_Note<T>> v)
118 {
119 //指针给指针赋值:右侧地址赋值给左侧地址(指针存储的是地址)
120 if (u->parent == nullptr) //如果u是根节点
121 root = v;
122 //都用 v替代u了 u的父节点不也被替代了么?---属于指针的赋值而不是类所以不用定于赋值运算符
123 else if (u == u->parent->left) //如果U是左孩子
124 u->parent->left = v;
125 else
126 u->parent->right = v;
127 if (v->parent != nullptr)
128 v->parent = u->parent;//不改变被替换树的上层
129 }
130 };
131
132 //成员函数定义在类外使用默认实参 报错:不允许使用默认参数
133 //原因(P271 《c++ prime 5th》):非静态数据成员不能作为默认实参:因为它的值本身属于对象的一部分,
134 //这么做的结果是:无法真正提供一个对象以便从中获取成员的值
135
136 //递归查找
137 template<typename T>
138 std::shared_ptr<Tree_Note<T>>
139 BST<T>::Tree_Search(const T& key,const std::shared_ptr<Tree_Note<T>> x)
140 {
141 if (x == nullptr || key == x->key)
142 return x;
143 if (key < x->key)//在左侧子树
144 return Tree_Search(key,x->left);
145 else//右侧子树
146 return Tree_Search(key,x->right);
147 }
148 //迭代查找:对于大多数计算机,迭代版本的效率要高的多 :调用函数开销
149 template<typename T>
150 std::shared_ptr<Tree_Note<T>>
151 BST<T>::Iterative_Tree_Search(const T& key,std::shared_ptr<Tree_Note<T>> x)
152 {
153 while (x != nullptr && key != x->key)
154 {
155 if (key < x->key)
156 x = x->left;
157 else
158 x = x->right;
159 }
160 return x;
161 }
162 //中序遍历
163 template<typename T>
164 void BST<T>::Iorder_Tree_Walk(const std::shared_ptr<Tree_Note<T>> x)
165 {
166 if (x != nullptr)
167 {
168 Iorder_Tree_Walk(x->left);
169 std::cout << x->key << " ";
170 Iorder_Tree_Walk(x->right);
171 }
172 }
173 //最小值
174 template<typename T>
175 std::shared_ptr<Tree_Note<T>>
176 BST<T>::Tree_Minimum(std::shared_ptr<Tree_Note<T>> x)
177 {
178 while (x->left != nullptr)
179 x = x->left;
180 return x;
181 }
182 //最大值
183 template<typename T>
184 std::shared_ptr<Tree_Note<T>>
185 BST<T>::Tree_Maximum(std::shared_ptr<Tree_Note<T>> x)
186 {
187 while (x->right != nullptr)
188 x = x->right;
189 return x;
190 }
191 //后继和前驱
192 template<typename T>
193 std::shared_ptr<Tree_Note<T>>
194 BST<T>::Tree_Successor(std::shared_ptr<Tree_Note<T>> x)
195 {
196 if (x->right != nullptr) // 对接近大于x的节点 处在右子树中最小值
197 return Tree_Minimum(x->right);
198 //从x开始向上寻找节点:该结点不是父节点的右孩子 (如果是右孩子则x.right不会为空)
199 auto y(x->parent);
200 while (y != nullptr && x == y->right)
201 {
202 x = y;
203 y = y->parent;
204 }
205 return y;//第一个不是右孩子的节点
206 }
207 template<typename T>
208 std::shared_ptr<Tree_Note<T>>
209 BST<T>::Tree_Predecessor(std::shared_ptr<Tree_Note<T>> x)
210 {
211 if (x->left != nullptr)
212 return Tree_Maximum(x->right);
213 auto y = x->parent;
214 while (y != nullptr && x == y->left)
215 {
216 x = y;
217 y = y->parent;
218 }
219 return y;
220 }
221
222 //插入和删除
223 template<typename T>
224 void BST<T>::Tree_Insert(std::shared_ptr<Tree_Note<T>> z)
225 {
226 //临时量用于确定z位置:不要调用make_shared 则不满足 !=nullptr 为空树时条件
227 std::shared_ptr<Tree_Note<T>> y = nullptr;
228 // auto y = std::make_shared<Tree_Note<T>>();
229 auto x(root);
230 //当x为空时,x就是待插入的位置
231 while (x != nullptr)
232 {
233 y = x;
234 if (z->key < x->key)
235 x = x->left;
236 else//包括相等的情况 具有稳定性:后插入的在右边
237 x = x->right;
238 }
239 z->parent = y;
240 if (y == nullptr)
241 root = z;
242 else if (z->key < y->key)
243 y->left = z;
244 else
245 y->right = z;
246 }
247
248 template<typename T>
249 void BST<T>::Tree_Delete(std::shared_ptr<Tree_Note<T>> z)
250 {
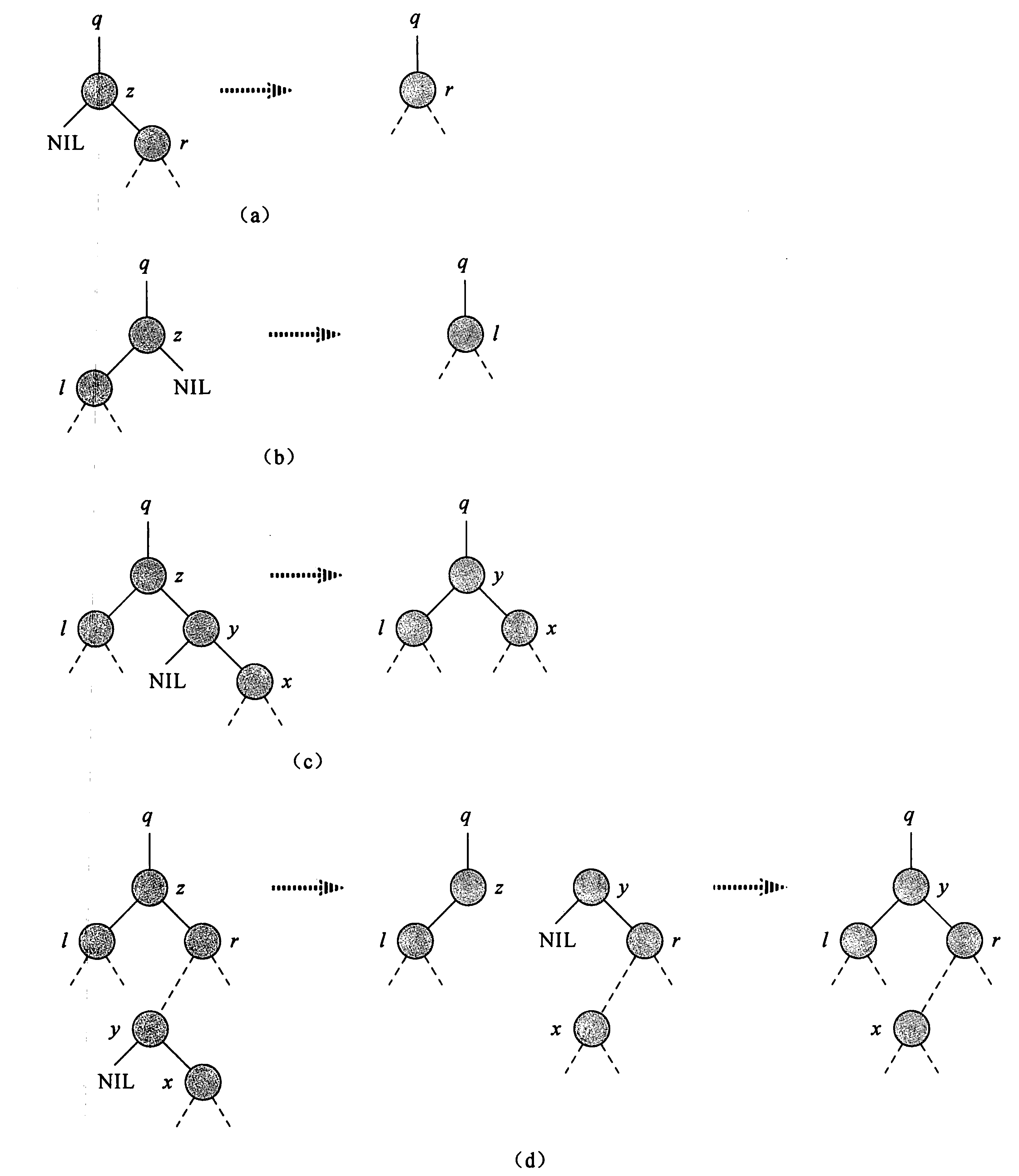
251 if (z->left == nullptr) //(a)
252 Transplant(z, z->right);
253 else if (z->right == nullptr) //(b)
254 Transplant(z, z->left);
255 else
256 {
257 auto y = Tree_Minimum(z->right);
258 if (y->parent != z) //(c):y不是z的右孩子
259 {
260 Transplant(y, y->right);
261 y->right = z->right;
262 y->right->parent = y;
263 }
264 //(d):y是z的右孩子 且y,left == nullptr 如果y的左孩子不是空则 y不是z的后继
265 Transplant(z, y);
266 y->left = z->left; //y的左孩子(拼接)指向被删除点z的左孩子
267 y->left->parent = y; //相当于 z = y
268 }
269 }
main
1 #include<iostream>
2 #include<vector>
3 #include"Binary_Seach_Tree.h"
4 using namespace std;
5
6 void BSTree()
7 {
8 vector<int> vi{ 1,2,5,8,6,9,6 };
9 BST<int> t;
10 //插入
11 for (auto i = 0;i != vi.size();++i)
12 t.Tree_Insert(vi[i]);
13 cout << "中序遍历" << endl;
14 t.Iorder_Tree_Walk();
15 cout << endl;
16 cout << "最大值" << endl;
17 cout << t.Tree_Maximum() << endl;
18 cout << "最小值" << endl;
19 cout << t.Tree_Minimum() << endl;
20 cout << "查找" << endl;
21 cout << boolalpha << t.Tree_Seach(8) << endl;
22 cout << "删除" << endl;
23 t.Tree_Delete(8);
24 cout << boolalpha << t.Iterative_Tree_Search(8) << endl;
25 }
26
27
28 int main()
29 {
30 BSTree();
31 return 0;
32 }
删除:form 《算法导论》 P167
关于其他操作请看二叉查找树(二)之 C++的实现