| 这个作业属于哪个班级 | 数据结构--网络2012 |
|---|---|
| 这个作业的地址 | DS博客作业03--树 |
| 这个作业的目标 | 学习树结构设计及运算操作 |
| 姓名 | 朱芳芳 |
0.PTA得分截图
树题目集总得分,请截图,截图中必须有自己名字。题目至少完成2/3,否则本次作业最高分5分。

1.本周学习总结(5分)
学习总结,请结合树的图形展开分析。
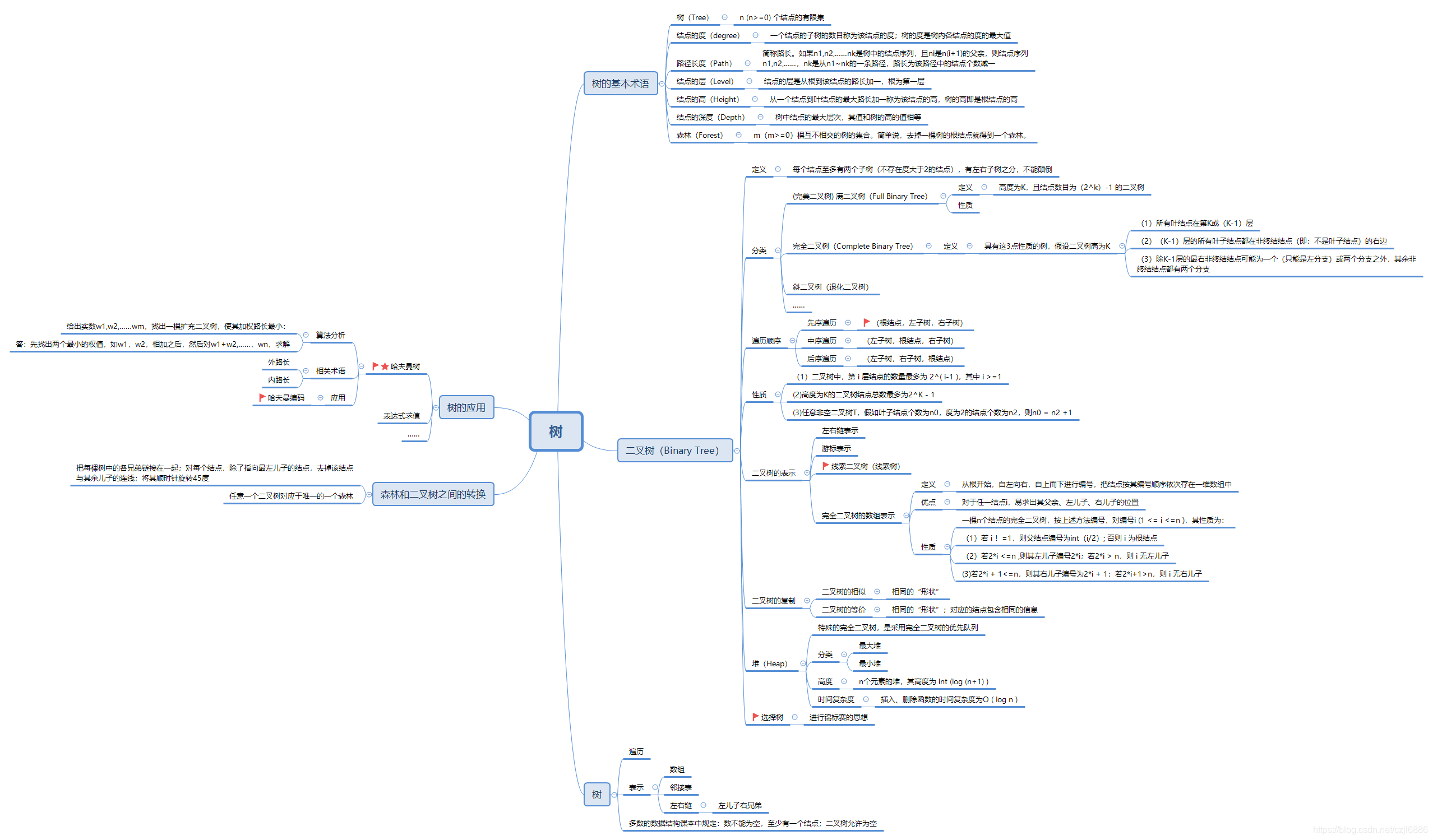
1.1 二叉树结构
1.1.1 二叉树的2种存储结构
树的顺序存储和链式存储结构,并分析优缺点。
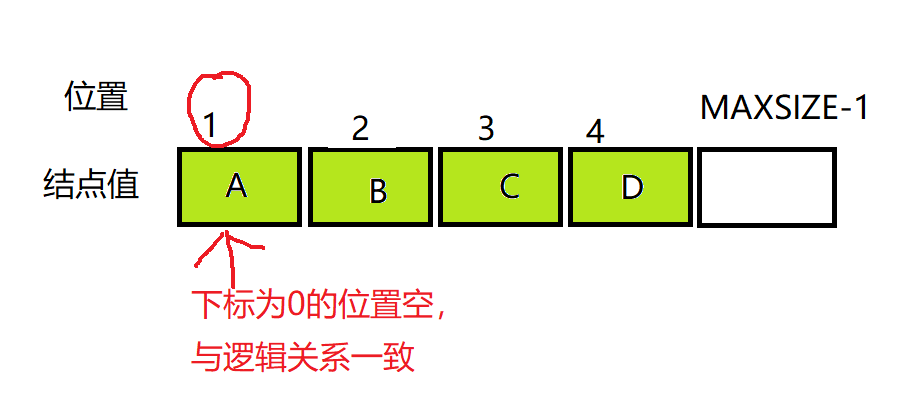
树的顺序存储结构
采用一组地址连续的存储单元来存放二叉树的数据元素(数组元素的下标关系反应完全二叉树中结点之间的逻辑关系)
关系如图
结构体如下

树的链式存储结构
二叉树的链式存储结构是指用一个链表来存储一棵二叉树,树的每一个结点用链表中的一个结点来存储。其中,data表示值域,用于存储对应的数据元素,lchild和rchild用来分别表示左指针域和右指针域,分别用于存储左孩子结点和右孩子结点的存储地址。
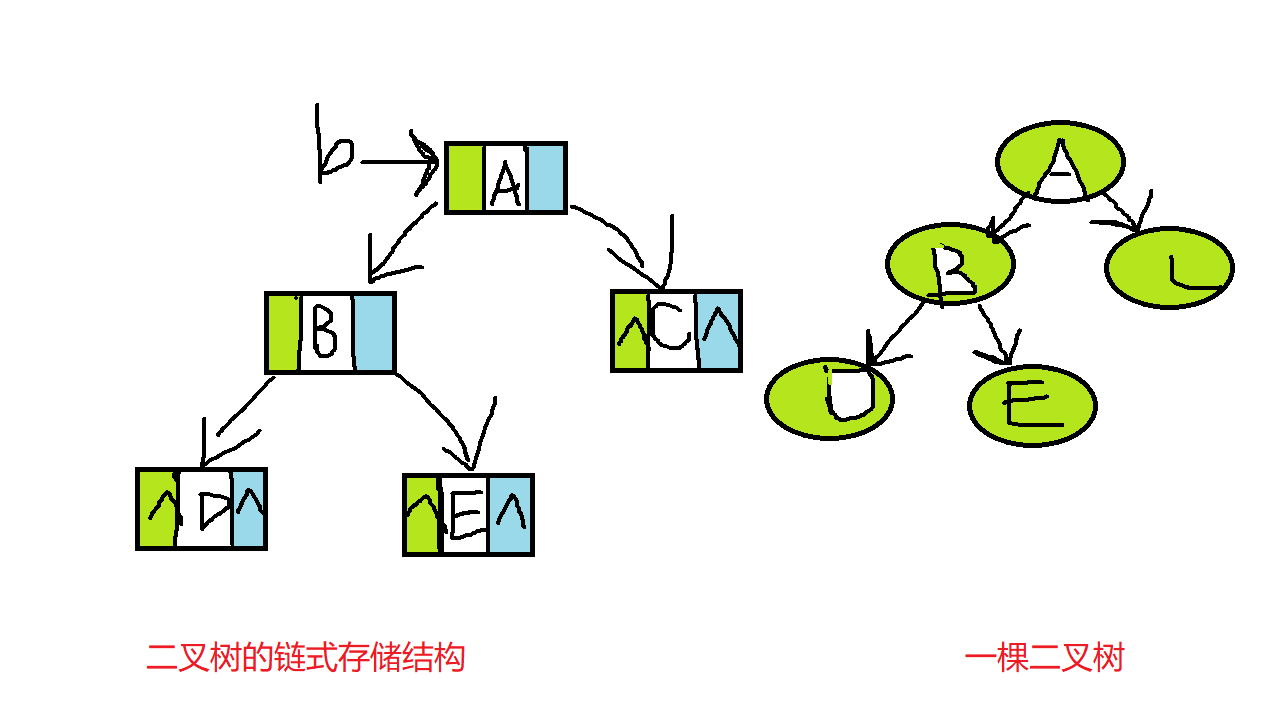
结构体如下

二者的优缺点:
二叉树的顺序存储结构
缺点:
1.具有顺序存储结构的固有缺陷,使得二叉树的插入,删除等运算操作十分不方便。(即需要移动大量数组元素)
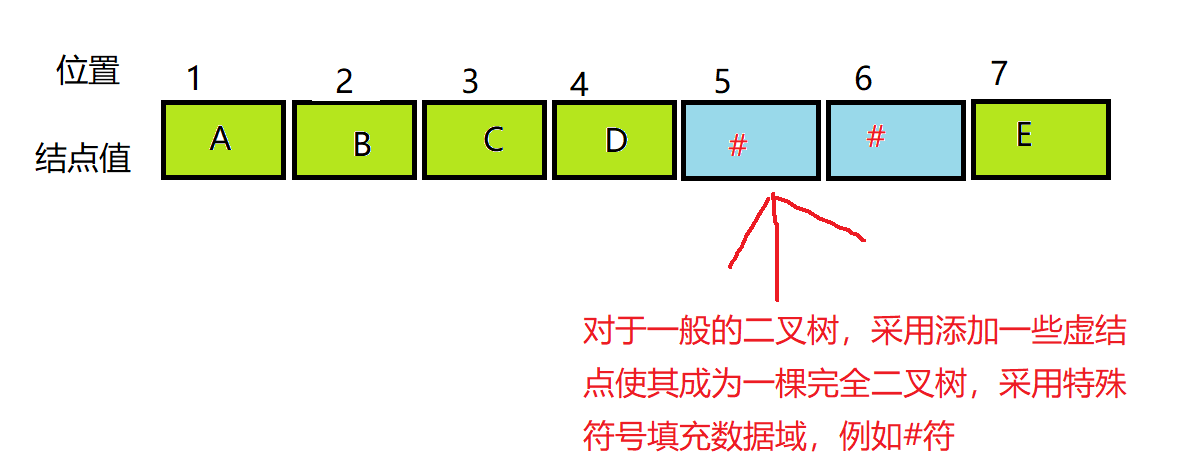
2.对于一般二叉树,采用此结构,需要增设大量空结点,造成空间浪费。
优点:
1.对于完全二叉树或者满二叉树采用此结构,能够最大可能节省存储空间,又可以利用数组元素的下标确定结点位置以及结点之间的关系,例如,
查找一个结点的孩子,双亲结点,高度,编号为i的结点的层次为log2(i+1)。
对于一个结点,如果有双亲,其双亲的下标编号为[i/2],如果有左孩子,则左孩子下标为[2i],如果有右孩子,则右孩子下标为[2i+1]。
二叉树的链式存储结构
优点:
对于一般二叉树,可以较大节省存储空间,在二叉链中访问一个结点的孩子很方便,
缺点:但访问他的双亲结点,则需要遍历所有节点。即,查找前驱结点很麻烦。
1.1.2 二叉树的构造
总结二叉树的几种构造方法。分析你对这些构造方法的看法。务必介绍如何通过先序遍历序列和中序遍历序列、后序遍历序列和中序遍历序列构造二叉树。
层次遍历构造
顺序转二叉链
1.1.3 二叉树的遍历
总结二叉树的4种遍历方式,如何实现。
前序遍历

中序遍历

后序遍历

层次遍历

1.1.4 线索二叉树
线索二叉树如何设计?
对于具有n个结点的二叉树,当采用二叉链存储结构是,每个结点具有两个指针域,总共有2n个指针域,又由于只有n-1个
结点被有效指针所指向(根结点没有),则共有2n-(n-1)个空链域,利用这些空链域存放指向结点的前驱结点的地址和
后继结点的地址,其规定是,当某结点的右指针为空时,令该指针指向这个线性序列中该结点的后继结点,反之前驱结点,即
左空前右空后表线索。采用在结点的存储结构上增加两个标志位来区分例如左指针指向的是前驱结点还是左孩子。
规定0表示指向孩子结点,1表示线索结点。

中序线索二叉树特点?
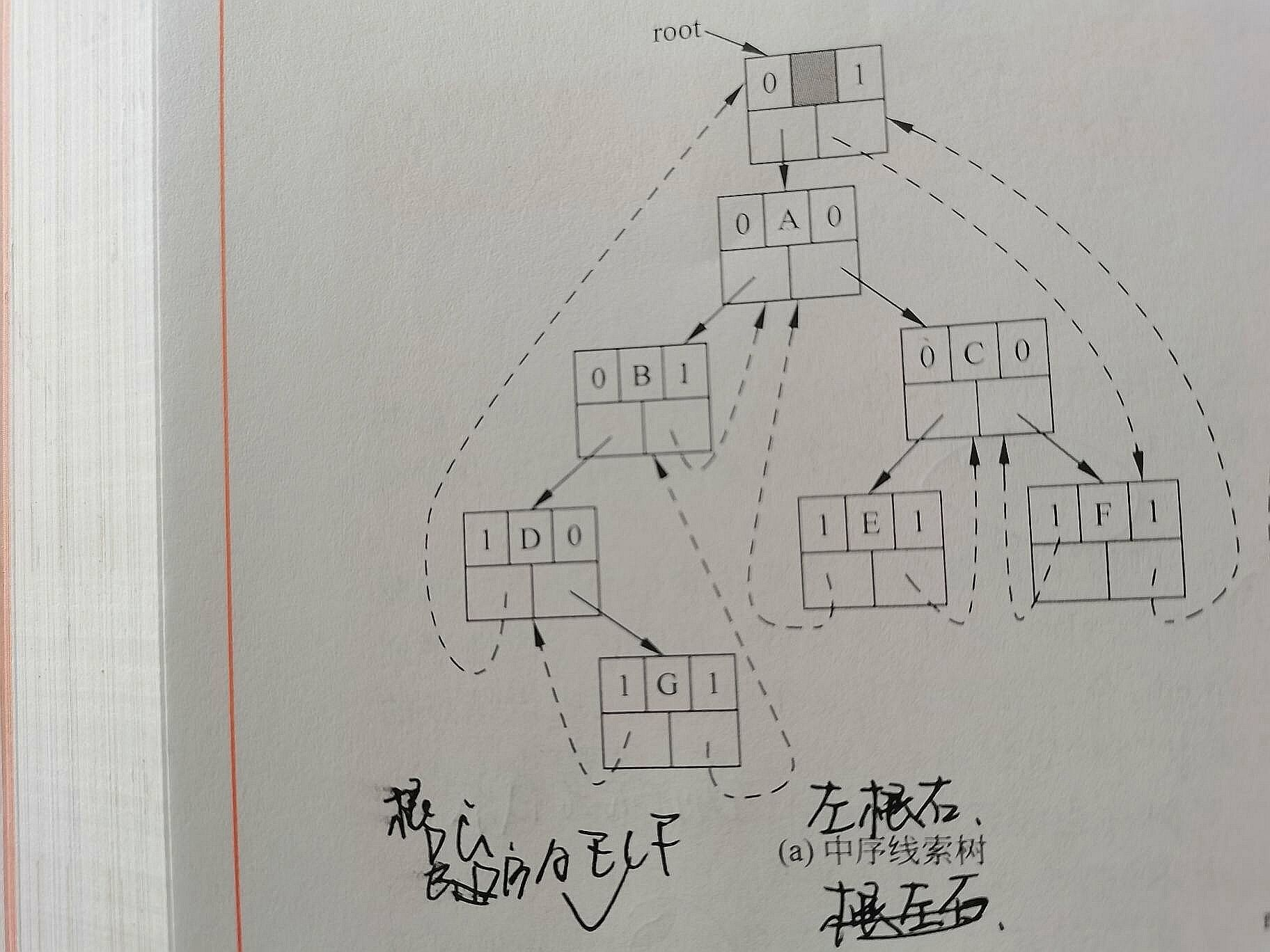
如何在中序线索二叉树查找前驱和后继?
1.1.5 二叉树的应用--表达式树
介绍表达式树如何构造
如何计算表达式树

1.2 多叉树结构
1.2.1 多叉树结构
主要介绍孩子兄弟链结构

1.2.2 多叉树遍历
介绍先序遍历做法
1.3 哈夫曼树
1.3.1 哈夫曼树定义
什么是哈夫曼树?,哈夫曼树解决什么问题?
在N0个带权叶子节点构成的所有二叉树中,带权路径长度WPL最小的二叉树,称为哈夫曼树,或最优二叉树。
哈夫曼树解决带权路径长度最小的问题,例如利用二叉树查找某一数据,某数据具有特定频率,哈夫曼树则将频率较高的数据存储在树的底层,减少遍历查找的时间。

1.3.2 哈夫曼树的结构体


教材是顺序存储结构,也可以自己搜索资料研究哈夫曼的链式结构设计方式。
1.3.2 哈夫曼树构建及哈夫曼编码

结合一组叶子节点的数据,介绍如何构造哈夫曼树及哈夫曼编码。
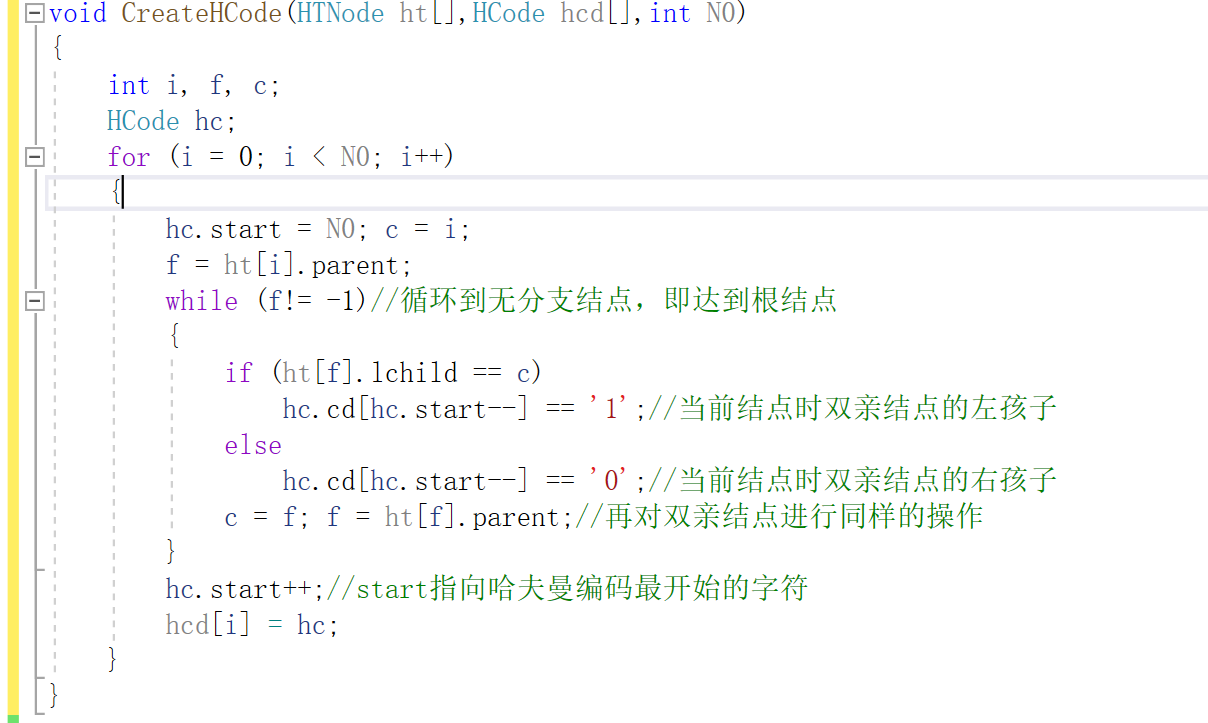
(可选)哈夫曼树代码设计,也可以参考链式设计方法。
1.4 并查集
什么是并查集?
当给出两个元素的一个无序对(a,b)时,需要快速“合并”a和b分别所在的集合,这期间需要反复“查找”某元素所在的集合,“并”,“查”,“集”由此而来。
在这种数据类型当中,n个不同的元素被分为若干组,每组是一个集合,这种集合叫做分离集合,称之为并查集。
并查集解决什么问题,优势在哪里?
并查集是一种数据类型???
(对于集合S中的关系R,若R具有自反,对称和传递性则称作等价关系,由等价关系R可以产生集合S的等价类)可以采用并查集高效求解等价类问题。
并查集的结构体、查找、合并操作如何实现?




1.5.谈谈你对树的认识及学习体会。
2.PTA实验作业(4分)
此处请放置下面2题代码所在码云地址(markdown插入代码所在的链接)。如何上传VS代码到码云
2.1 二叉树
输出二叉树每层节点、二叉表达式树、二叉树叶子结点带权路径长度和 三题自选一题介绍。
2.1.1 解题思路及伪代码



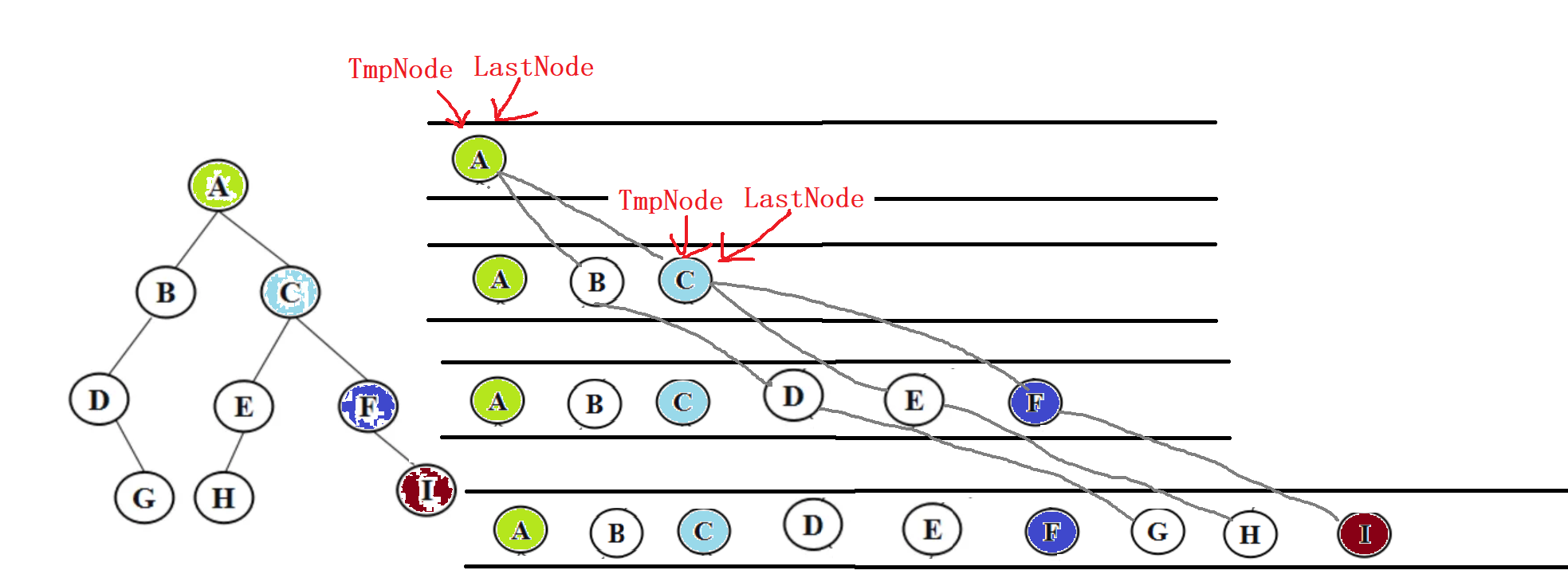
2.1.2 总结解题所用的知识点
该题综合运用到了队列,树和指针的知识。
层次遍历无需使用递归,而是采用队列的方式,实现先进先出,正好满足树先左子树再右子树的逻辑顺序,
对于换行的判断,使用标志变量来判断
2.2 目录树
https://paste.ubuntu.com/p/zVNxHzgFqR/
2.2.1 解题思路及伪代码

结构体




2.2.2 总结解题所用的知识点
在对字符串进行切片的算法中,采用到了字符串的一些属性方法,例如拷贝,查找等
插入结点算法中,缩进机制的考虑,只需考虑孩子结点,无需考虑兄弟结点
3.阅读代码(0--1分)
找1份优秀代码,理解代码功能,并讲出你所选代码优点及可以学习地方。主要找以下类型代码:
考研题
蓝桥杯题解,这个连接只是参考的题目,具体可以自己搜索蓝桥杯,查看历年的题解。只能找树相关题目介绍。
leecode--树
注意:不能选教师布置在PTA的题目。完成内容如下。
3.1 题目及解题代码
可截图,或复制代码,需要用代码符号渲染。

3.2 该题的设计思路及伪代码
请用图形方式展示解决方法。同时分析该题的算法时间复杂度和空间复杂度。
解题思路:
此题属于二叉树节点删除问题的实际应用,并且结合深度优先搜索(前序遍历的应用)和回溯的思想