Code-force 1003 E Tree Constructing

                                                                                                E. Tree Constructing

You are given three integers $\mathrm{nn, dd and kk.}$

Your task is to construct an undirected tree on $\mathrm{nn vertices\; with\; diameter dd and\; degree\; of\; each\; vertex\; at\; most kk,\; or\; say\; that\; it\; is\; impossible.}$

An undirected tree is a connected undirected graph with $\mathrm{n-1n-1 edges.}$

Diameter of a tree is the maximum length of a simple path (a path in which each vertex appears at most once) between all pairs of vertices of this tree.

Degree of a vertex is the number of edges incident to this vertex (i.e. for a vertex $\mathrm{uu it\; is\; the\; number\; of\; edges (u,v)(u,v) that\; belong\; to\; the\; tree,\; where vv is\; any\; other\; vertex\; of\; a\; tree).}$

Input

The first line of the input contains three integers $\mathrm{nn, dd and kk (1\le n,d,k\le 4\cdot 1051\le n,d,k\le 4\cdot 105).}$

Output

If there is no tree satisfying the conditions above, print only one word "NO" (without quotes).

Otherwise in the first line print "YES" (without quotes), and then print $\mathrm{n-1n-1 lines\; describing\; edges\; of\; a\; tree\; satisfying\; the\; conditions\; above.\; Vertices\; of\; the\; tree\; must\; be\; numbered\; from 11 to nn.\; You\; can\; print\; edges\; and\; vertices\; connected\; by\; an\; edge\; in\; any\; order.\; If\; there\; are\; multiple\; answers,\; print\; any\; of\; them.1}$

$\mathrm{题意：}$

$\mathrm{要构建一颗树，树的直径要是d，就是树上的节点最远的距离为d，每个节点的度最多为k,一共有n个节点。}$

$\mathrm{思路：}$

$\mathrm{先判断可不可以建出符合要求的树，可以的话，先把直径建好，再到这条直径上挂上子树。}$

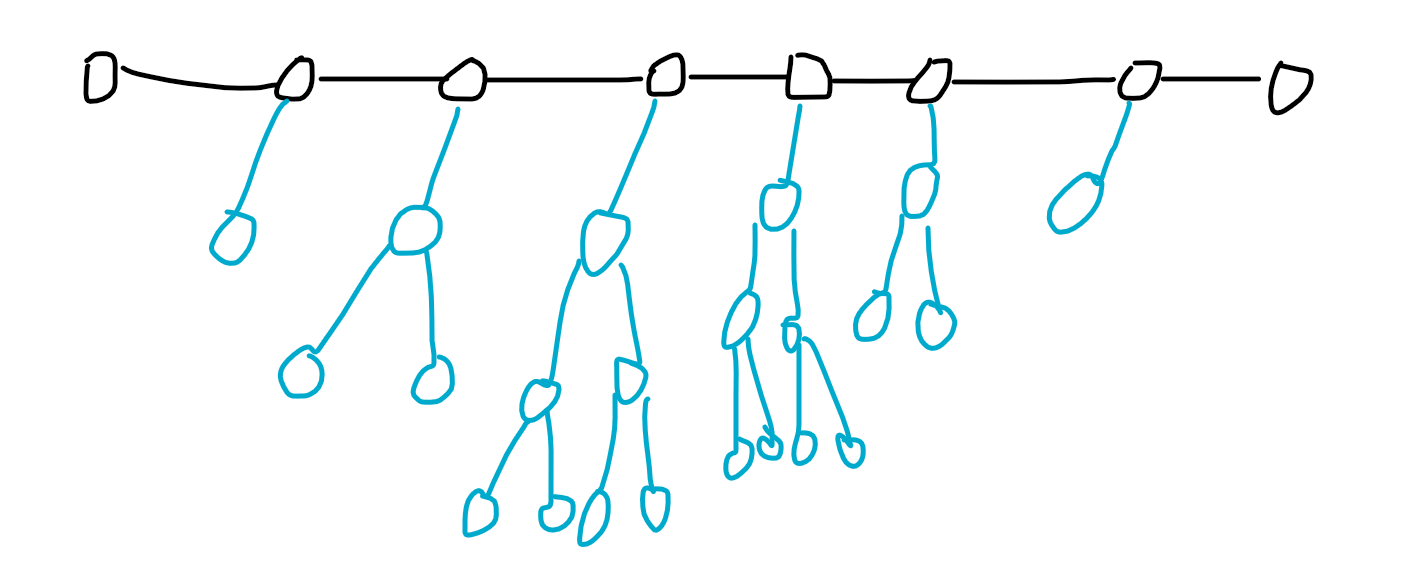
　　注意子树的深度变化，还有建树的过程中，并不一定是建的如此之满，所以当节点数用完时，要及时退出。

AC代码（C++）

#include<iostream>
#include<queue>
using namespace std;
int n,d,k,flag,t;
int quick_pow(int a,int b)
{
    int ans=0,t=1;
    for(int i=0;i<b;i++){
        t*=a;
        ans+=t;
        if(ans>=n){return -1;}
    }
    return ans;
}

void build(int s,int h,int de)//de是子树的深度，s是父节点
{
    if(h>de){return;}
    if(t>=n){return;}
    t++;
    printf("%d %d
",s,t);
    if(t>=n){return;}
    int o=t;
    if(h>de-1){return;}
    for(int i=0;i<k-1;i++){
        build(o,h+1,de);
        if(t>=n){return;}
    }
}

int main()
{
    scanf("%d%d%d",&n,&d,&k);
    if(n<d+1){printf("NO");return 0;}
    if(d&1){
        t=quick_pow(k-1,d/2);
        if(t==-1){printf("YES
");}
        else{
            t=2*(t+1);
            if(t<n){printf("NO");return 0;}
        }
    }
    else {
        t=quick_pow(k-1,d/2-1);
        if(t==-1){printf("YES
");}
        else{
            t=k*t+1+k;
            if(t<n){printf("NO");return 0;}
        }
    }
    if(t!=-1){printf("YES
");}
    int de=-1;
    t=d+1;
    for(int i=1;i<=d;i++){
        printf("%d %d
",i,i+1);
        if(t>=n){continue;}
        if(d&1){
            if(i<=d/2+1){de++;}
            else if(i>d/2+2){de--;}
        }
        else {
            if(i<=d/2+1){de++;}
            else de--;
        }
        for(int j=0;j<k-2;j++){
            build(i,1,de);if(t>=n){break;}
        }
    }
}